GrassNet: State Space Model Meets Graph Neural Network
Paper and Code
Aug 16, 2024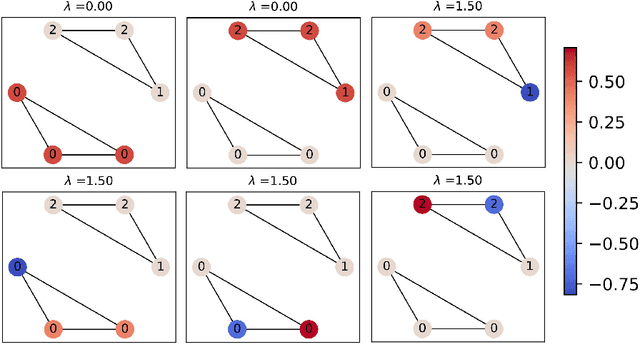


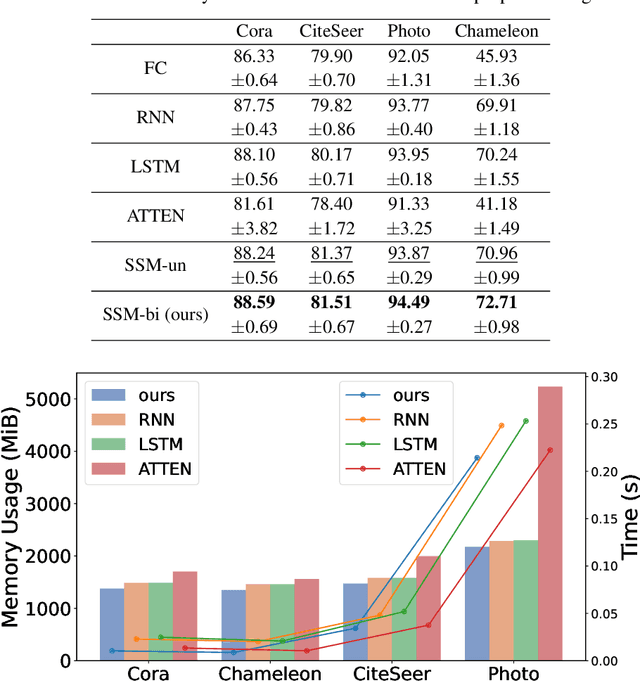
Designing spectral convolutional networks is a formidable task in graph learning. In traditional spectral graph neural networks (GNNs), polynomial-based methods are commonly used to design filters via the Laplacian matrix. In practical applications, however, these polynomial methods encounter inherent limitations, which primarily arise from the the low-order truncation of polynomial filters and the lack of overall modeling of the graph spectrum. This leads to poor performance of existing spectral approaches on real-world graph data, especially when the spectrum is highly concentrated or contains many numerically identical values, as they tend to apply the exact same modulation to signals with the same frequencies. To overcome these issues, in this paper, we propose Graph State Space Network (GrassNet), a novel graph neural network with theoretical support that provides a simple yet effective scheme for designing and learning arbitrary graph spectral filters. In particular, our GrassNet introduces structured state space models (SSMs) to model the correlations of graph signals at different frequencies and derives a unique rectification for each frequency in the graph spectrum. To the best of our knowledge, our work is the first to employ SSMs for the design of GNN spectral filters, and it theoretically offers greater expressive power compared with polynomial filters. Extensive experiments on nine public benchmarks reveal that GrassNet achieves superior performance in real-world graph modeling tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge