Gradient-Based Mixed Planning with Discrete and Continuous Actions

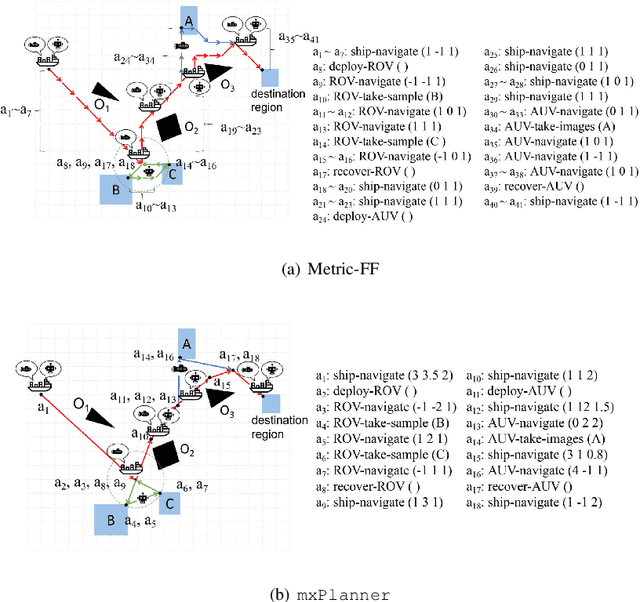
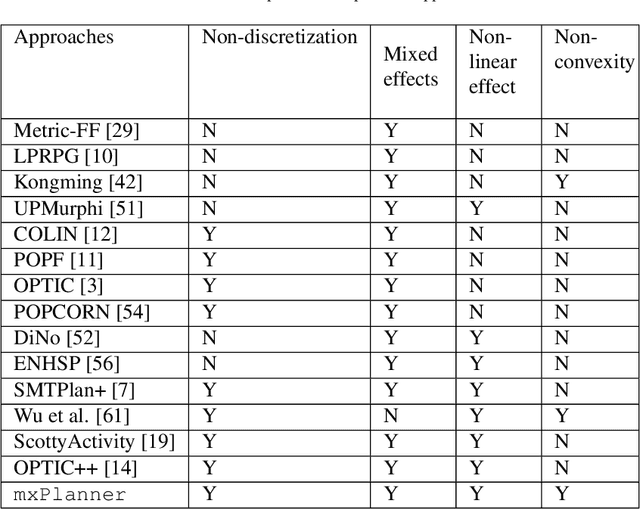
Dealing with planning problems with both discrete logical relations and continuous numeric changes in real-world dynamic environments is challenging. Existing numeric planning systems for the problem often discretize numeric variables or impose convex quadratic constraints on numeric variables, which harms the performance when solving the problem. In this paper, we propose a novel algorithm framework to solve the numeric planning problems mixed with discrete and continuous actions based on gradient descent. We cast the numeric planning with discrete and continuous actions as an optimization problem by integrating a heuristic function based on discrete effects. Specifically, we propose a gradient-based framework to simultaneously optimize continuous parameters and actions of candidate plans. The framework is combined with a heuristic module to estimate the best plan candidate to transit initial state to the goal based on relaxation. We repeatedly update numeric parameters and compute candidate plan until it converges to a valid plan to the planning problem. In the empirical study, we exhibit that our algorithm framework is both effective and efficient, especially when solving non-convex planning problems.