Gradient-based Label Binning in Multi-label Classification
Paper and Code
Jun 22, 2021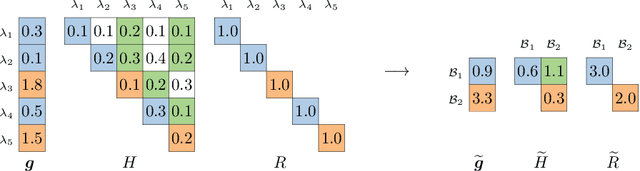
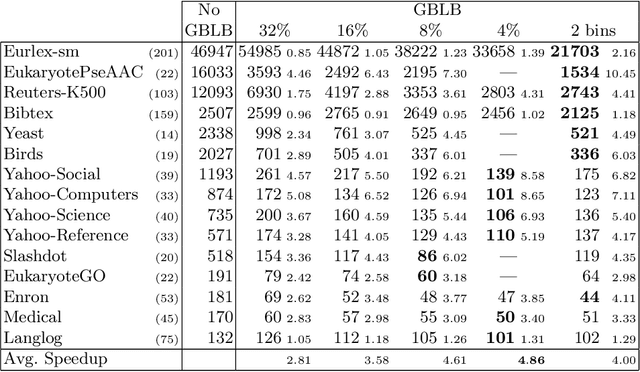
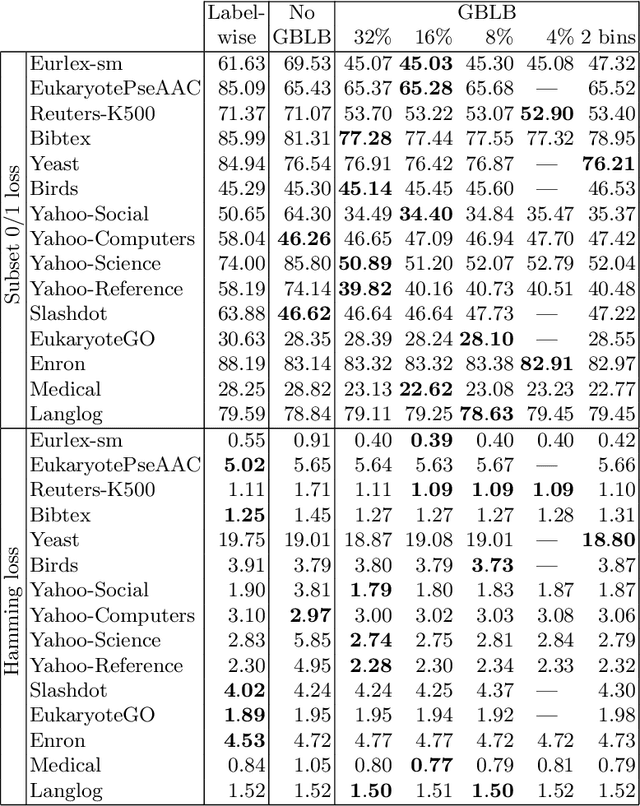
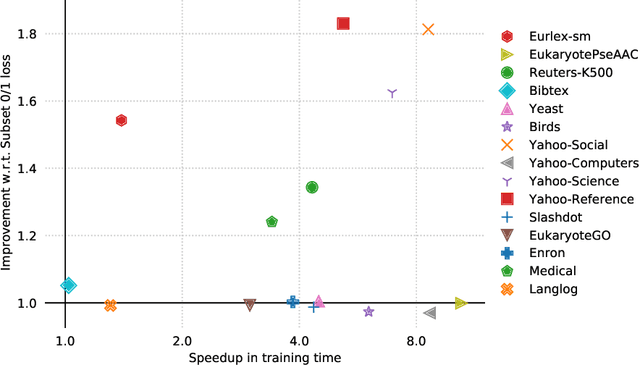
In multi-label classification, where a single example may be associated with several class labels at the same time, the ability to model dependencies between labels is considered crucial to effectively optimize non-decomposable evaluation measures, such as the Subset 0/1 loss. The gradient boosting framework provides a well-studied foundation for learning models that are specifically tailored to such a loss function and recent research attests the ability to achieve high predictive accuracy in the multi-label setting. The utilization of second-order derivatives, as used by many recent boosting approaches, helps to guide the minimization of non-decomposable losses, due to the information about pairs of labels it incorporates into the optimization process. On the downside, this comes with high computational costs, even if the number of labels is small. In this work, we address the computational bottleneck of such approach -- the need to solve a system of linear equations -- by integrating a novel approximation technique into the boosting procedure. Based on the derivatives computed during training, we dynamically group the labels into a predefined number of bins to impose an upper bound on the dimensionality of the linear system. Our experiments, using an existing rule-based algorithm, suggest that this may boost the speed of training, without any significant loss in predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge