GM-PLL: Graph Matching based Partial Label Learning
Paper and Code
Jan 10, 2019
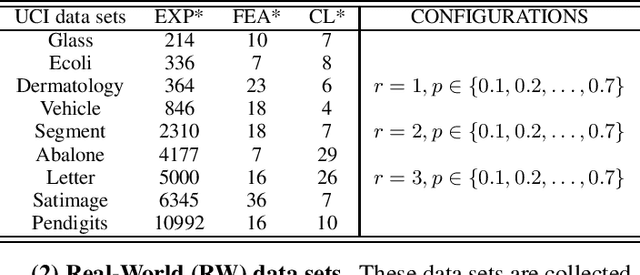
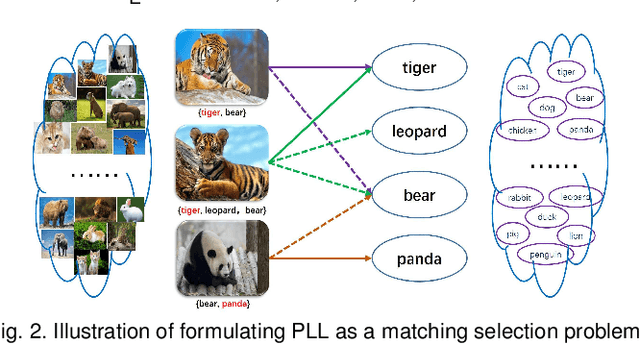
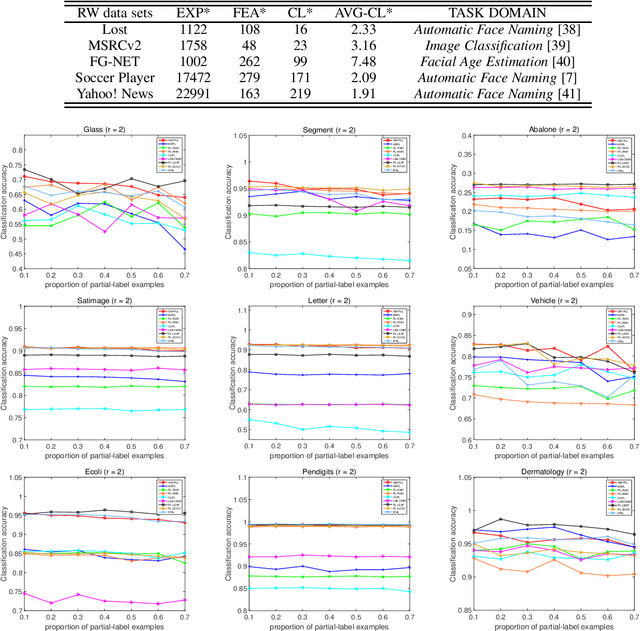
Partial Label Learning (PLL) aims to learn from the data where each training example is associated with a set of candidate labels, among which only one is correct. The key to deal with such problem is to disambiguate the candidate label sets and obtain the correct assignments between instances and their candidate labels. In this paper, we interpret such assignments as instance-to-label matchings, and reformulate the task of PLL as a matching selection problem. To model such problem, we propose a novel Graph Matching based Partial Label Learning (GM-PLL) framework, where Graph Matching (GM) scheme is incorporated owing to its excellent capability of exploiting the instance and label relationship. Meanwhile, since conventional one-to-one GM algorithm does not satisfy the constraint of PLL problem that multiple instances may correspond to the same label, we extend a traditional one-to-one probabilistic matching algorithm to the many-to-one constraint, and make the proposed framework accommodate to the PLL problem. Moreover, we also propose a relaxed matching prediction model, which can improve the prediction accuracy via GM strategy. Extensive experiments on both artificial and real-world data sets demonstrate that the proposed method can achieve superior or comparable performance against the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge