Geometrically Principled Connections in Graph Neural Networks

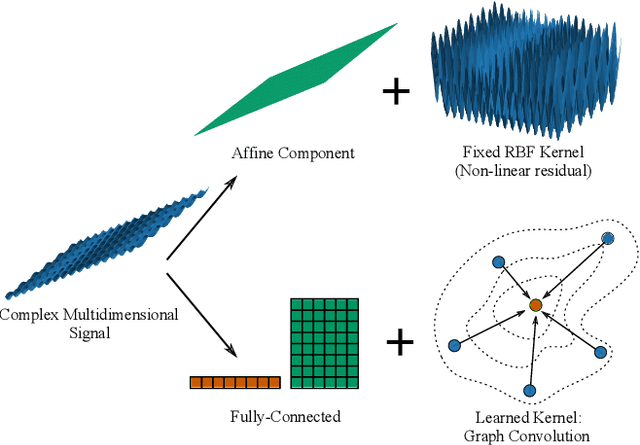
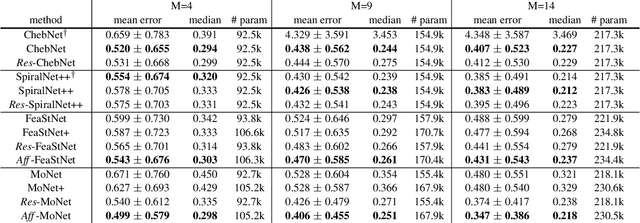
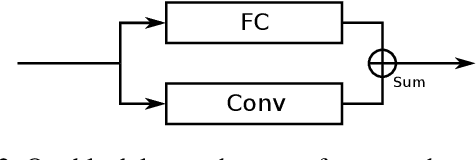
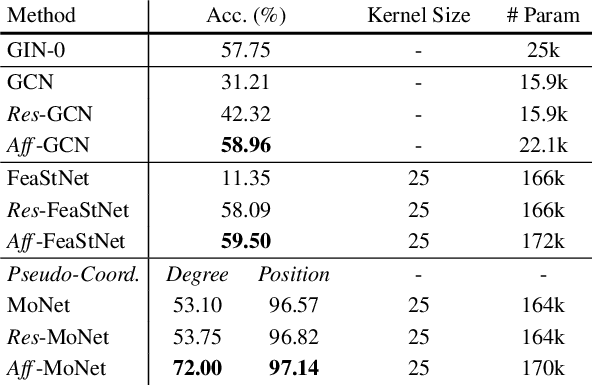
Graph convolution operators bring the advantages of deep learning to a variety of graph and mesh processing tasks previously deemed out of reach. With their continued success comes the desire to design more powerful architectures, often by adapting existing deep learning techniques to non-Euclidean data. In this paper, we argue geometry should remain the primary driving force behind innovation in the emerging field of geometric deep learning. We relate graph neural networks to widely successful computer graphics and data approximation models: radial basis functions (RBFs). We conjecture that, like RBFs, graph convolution layers would benefit from the addition of simple functions to the powerful convolution kernels. We introduce affine skip connections, a novel building block formed by combining a fully connected layer with any graph convolution operator. We experimentally demonstrate the effectiveness of our technique and show the improved performance is the consequence of more than the increased number of parameters. Operators equipped with the affine skip connection markedly outperform their base performance on every task we evaluated, i.e., shape reconstruction, dense shape correspondence, and graph classification. We hope our simple and effective approach will serve as a solid baseline and help ease future research in graph neural networks.