Generative Modelling of Stochastic Actions with Arbitrary Constraints in Reinforcement Learning
Paper and Code
Nov 26, 2023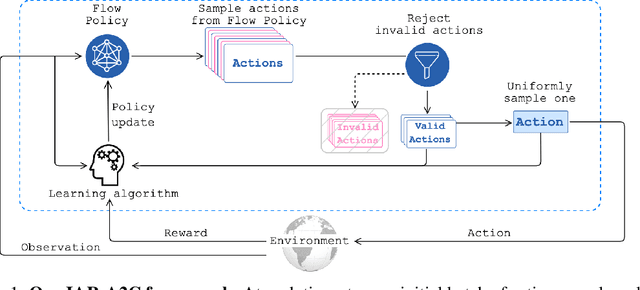
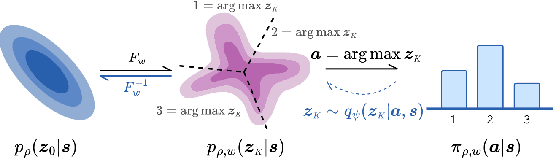
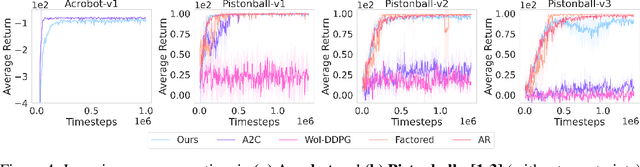
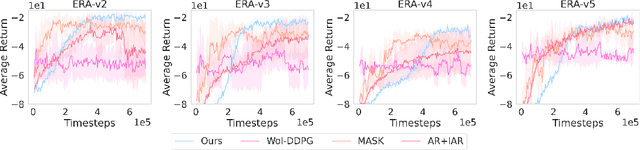
Many problems in Reinforcement Learning (RL) seek an optimal policy with large discrete multidimensional yet unordered action spaces; these include problems in randomized allocation of resources such as placements of multiple security resources and emergency response units, etc. A challenge in this setting is that the underlying action space is categorical (discrete and unordered) and large, for which existing RL methods do not perform well. Moreover, these problems require validity of the realized action (allocation); this validity constraint is often difficult to express compactly in a closed mathematical form. The allocation nature of the problem also prefers stochastic optimal policies, if one exists. In this work, we address these challenges by (1) applying a (state) conditional normalizing flow to compactly represent the stochastic policy -- the compactness arises due to the network only producing one sampled action and the corresponding log probability of the action, which is then used by an actor-critic method; and (2) employing an invalid action rejection method (via a valid action oracle) to update the base policy. The action rejection is enabled by a modified policy gradient that we derive. Finally, we conduct extensive experiments to show the scalability of our approach compared to prior methods and the ability to enforce arbitrary state-conditional constraints on the support of the distribution of actions in any state.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge