Gaussian Mixture Convolution Networks
Paper and Code
Feb 18, 2022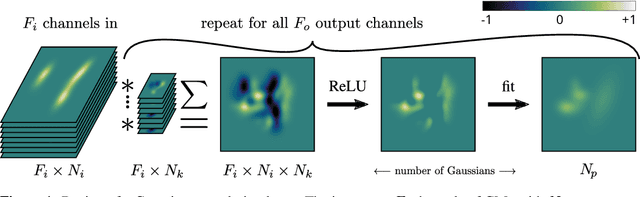
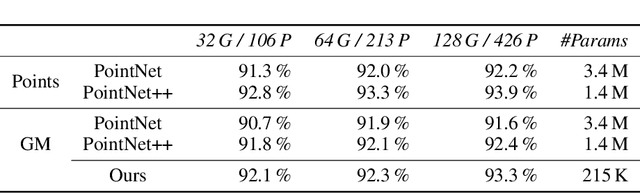


This paper proposes a novel method for deep learning based on the analytical convolution of multidimensional Gaussian mixtures. In contrast to tensors, these do not suffer from the curse of dimensionality and allow for a compact representation, as data is only stored where details exist. Convolution kernels and data are Gaussian mixtures with unconstrained weights, positions, and covariance matrices. Similar to discrete convolutional networks, each convolution step produces several feature channels, represented by independent Gaussian mixtures. Since traditional transfer functions like ReLUs do not produce Gaussian mixtures, we propose using a fitting of these functions instead. This fitting step also acts as a pooling layer if the number of Gaussian components is reduced appropriately. We demonstrate that networks based on this architecture reach competitive accuracy on Gaussian mixtures fitted to the MNIST and ModelNet data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge