Gaussian meta-embeddings for efficient scoring of a heavy-tailed PLDA model
Paper and Code
Feb 27, 2018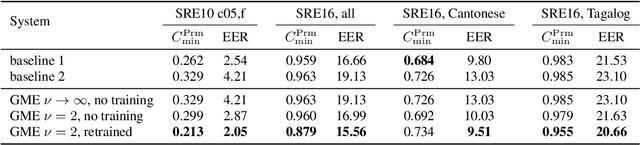
Embeddings in machine learning are low-dimensional representations of complex input patterns, with the property that simple geometric operations like Euclidean distances and dot products can be used for classification and comparison tasks. The proposed meta-embeddings are special embeddings that live in more general inner product spaces. They are designed to propagate uncertainty to the final output in speaker recognition and similar applications. The familiar Gaussian PLDA model (GPLDA) can be re-formulated as an extractor for Gaussian meta-embeddings (GMEs), such that likelihood ratio scores are given by Hilbert space inner products between Gaussian likelihood functions. GMEs extracted by the GPLDA model have fixed precisions and do not propagate uncertainty. We show that a generalization to heavy-tailed PLDA gives GMEs with variable precisions, which do propagate uncertainty. Experiments on NIST SRE 2010 and 2016 show that the proposed method applied to i-vectors without length normalization is up to 20% more accurate than GPLDA applied to length-normalized ivectors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge