GAP: Differentially Private Graph Neural Networks with Aggregation Perturbation

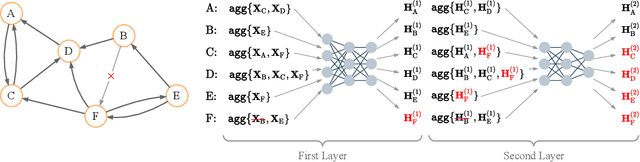
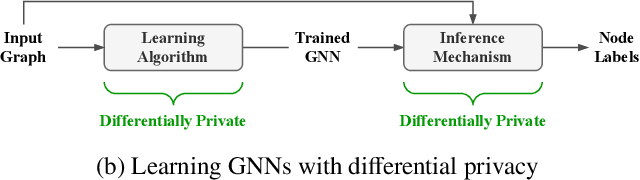
Graph Neural Networks (GNNs) are powerful models designed for graph data that learn node representation by recursively aggregating information from each node's local neighborhood. However, despite their state-of-the-art performance in predictive graph-based applications, recent studies have shown that GNNs can raise significant privacy concerns when graph data contain sensitive information. As a result, in this paper, we study the problem of learning GNNs with Differential Privacy (DP). We propose GAP, a novel differentially private GNN that safeguards the privacy of nodes and edges using aggregation perturbation, i.e., adding calibrated stochastic noise to the output of the GNN's aggregation function, which statistically obfuscates the presence of a single edge (edge-level privacy) or a single node and all its adjacent edges (node-level privacy). To circumvent the accumulation of privacy cost at every forward pass of the model, we tailor the GNN architecture to the specifics of private learning. In particular, we first precompute private aggregations by recursively applying neighborhood aggregation and perturbing the output of each aggregation step. Then, we privately train a deep neural network on the resulting perturbed aggregations for any node-wise classification task. A major advantage of GAP over previous approaches is that we guarantee edge-level and node-level DP not only for training, but also at inference time with no additional costs beyond the training's privacy budget. We theoretically analyze the formal privacy guarantees of GAP using R\'enyi DP. Empirical experiments conducted over three real-world graph datasets demonstrate that GAP achieves a favorable privacy-accuracy trade-off and significantly outperforms existing approaches.