Game-Theoretic Algorithms for Conditional Moment Matching
Paper and Code
Aug 19, 2022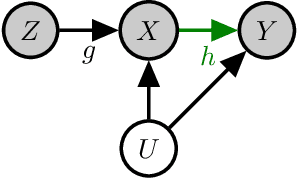
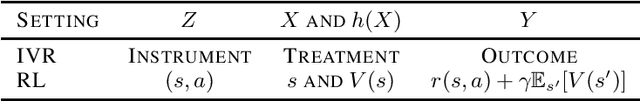
A variety of problems in econometrics and machine learning, including instrumental variable regression and Bellman residual minimization, can be formulated as satisfying a set of conditional moment restrictions (CMR). We derive a general, game-theoretic strategy for satisfying CMR that scales to nonlinear problems, is amenable to gradient-based optimization, and is able to account for finite sample uncertainty. We recover the approaches of Dikkala et al. and Dai et al. as special cases of our general framework before detailing various extensions and how to efficiently solve the game defined by CMR.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge