GA-SAM: Gradient-Strength based Adaptive Sharpness-Aware Minimization for Improved Generalization
Paper and Code
Oct 13, 2022
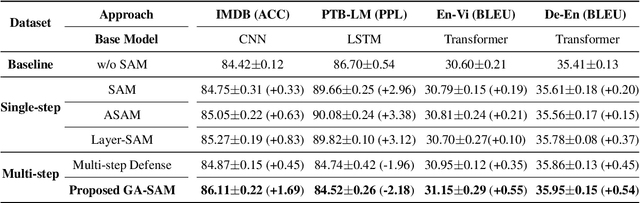


Recently, Sharpness-Aware Minimization (SAM) algorithm has shown state-of-the-art generalization abilities in vision tasks. It demonstrates that flat minima tend to imply better generalization abilities. However, it has some difficulty implying SAM to some natural language tasks, especially to models with drastic gradient changes, such as RNNs. In this work, we analyze the relation between the flatness of the local minimum and its generalization ability from a novel and straightforward theoretical perspective. We propose that the shift of the training and test distributions can be equivalently seen as a virtual parameter corruption or perturbation, which can explain why flat minima that are robust against parameter corruptions or perturbations have better generalization performances. On its basis, we propose a Gradient-Strength based Adaptive Sharpness-Aware Minimization (GA-SAM) algorithm to help to learn algorithms find flat minima that generalize better. Results in various language benchmarks validate the effectiveness of the proposed GA-SAM algorithm on natural language tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge