Fundamental Limits of Communication Efficiency for Model Aggregation in Distributed Learning: A Rate-Distortion Approach
Paper and Code
Jun 28, 2022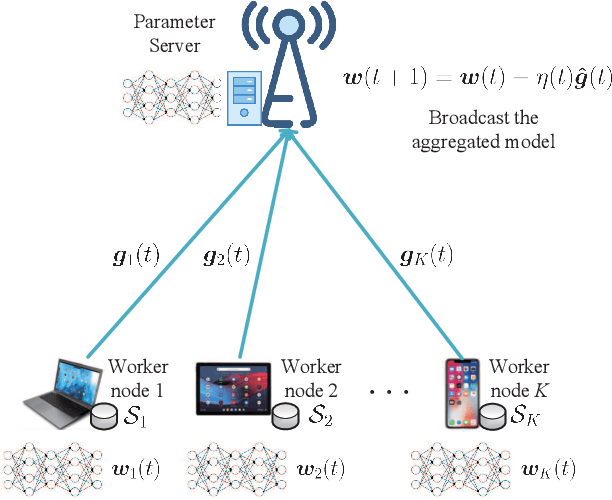
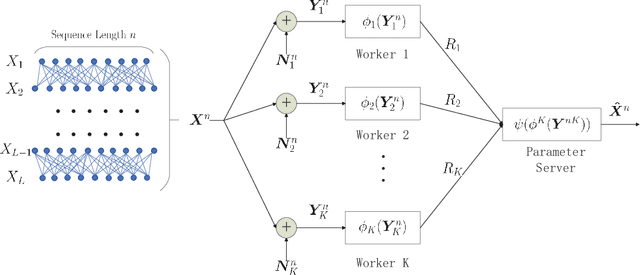
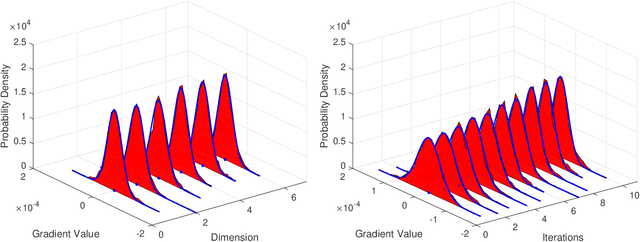
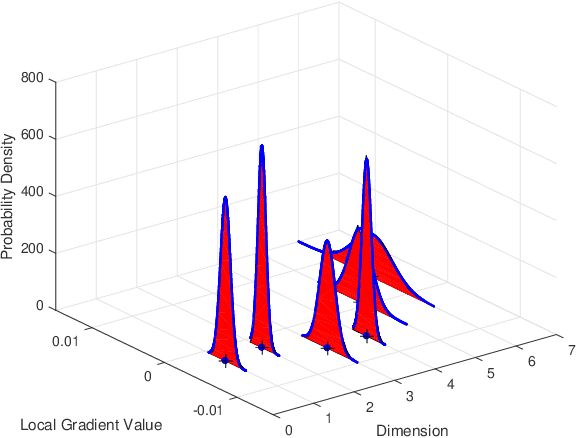
One of the main focuses in distributed learning is communication efficiency, since model aggregation at each round of training can consist of millions to billions of parameters. Several model compression methods, such as gradient quantization and sparsification, have been proposed to improve the communication efficiency of model aggregation. However, the information-theoretic minimum communication cost for a given distortion of gradient estimators is still unknown. In this paper, we study the fundamental limit of communication cost of model aggregation in distributed learning from a rate-distortion perspective. By formulating the model aggregation as a vector Gaussian CEO problem, we derive the rate region bound and sum-rate-distortion function for the model aggregation problem, which reveals the minimum communication rate at a particular gradient distortion upper bound. We also analyze the communication cost at each iteration and total communication cost based on the sum-rate-distortion function with the gradient statistics of real-world datasets. It is found that the communication gain by exploiting the correlation between worker nodes is significant for SignSGD, and a high distortion of gradient estimator can achieve low total communication cost in gradient compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge