From Continuous Dynamics to Graph Neural Networks: Neural Diffusion and Beyond
Paper and Code
Oct 29, 2023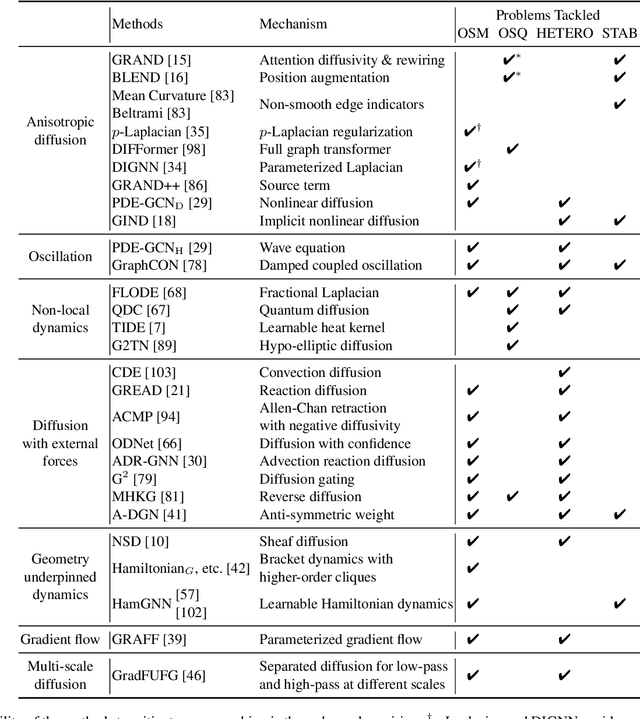
Graph neural networks (GNNs) have demonstrated significant promise in modelling relational data and have been widely applied in various fields of interest. The key mechanism behind GNNs is the so-called message passing where information is being iteratively aggregated to central nodes from their neighbourhood. Such a scheme has been found to be intrinsically linked to a physical process known as heat diffusion, where the propagation of GNNs naturally corresponds to the evolution of heat density. Analogizing the process of message passing to the heat dynamics allows to fundamentally understand the power and pitfalls of GNNs and consequently informs better model design. Recently, there emerges a plethora of works that proposes GNNs inspired from the continuous dynamics formulation, in an attempt to mitigate the known limitations of GNNs, such as oversmoothing and oversquashing. In this survey, we provide the first systematic and comprehensive review of studies that leverage the continuous perspective of GNNs. To this end, we introduce foundational ingredients for adapting continuous dynamics to GNNs, along with a general framework for the design of graph neural dynamics. We then review and categorize existing works based on their driven mechanisms and underlying dynamics. We also summarize how the limitations of classic GNNs can be addressed under the continuous framework. We conclude by identifying multiple open research directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge