Fix Your Features: Stationary and Maximally Discriminative Embeddings using Regular Polytope (Fixed Classifier) Networks
Paper and Code
Mar 01, 2019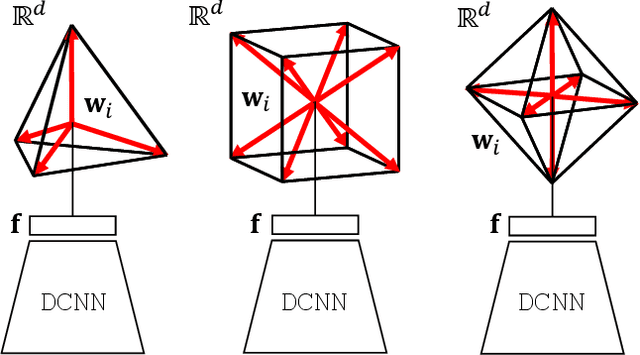

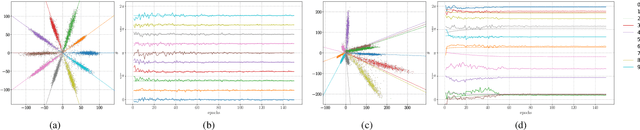
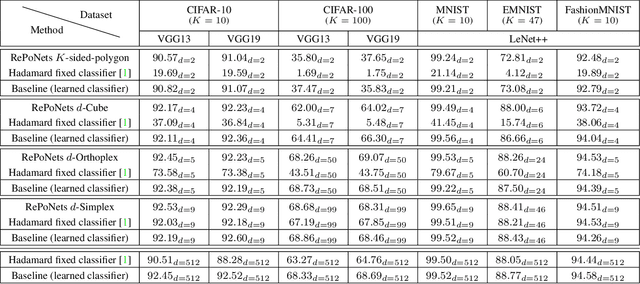
Neural networks are widely used as a model for classification in a large variety of tasks. Typically, a learnable transformation (i.e. the classifier) is placed at the end of such models returning a value for each class used for classification. This transformation plays an important role in determining how the generated features change during the learning process. In this work we argue that this transformation not only can be fixed (i.e. set as non trainable) with no loss of accuracy, but it can also be used to learn stationary and maximally discriminative embeddings. We show that the stationarity of the embedding and its maximal discriminative representation can be theoretically justified by setting the weights of the fixed classifier to values taken from the coordinate vertices of three regular polytopes available in $\mathbb{R}^d$, namely: the $d$-Simplex, the $d$-Cube and the $d$-Orthoplex. These regular polytopes have the maximal amount of symmetry that can be exploited to generate stationary features angularly centered around their corresponding fixed weights. Our approach improves and broadens the concept of a fixed classifier, recently proposed in \cite{hoffer2018fix}, to a larger class of fixed classifier models. Experimental results confirm both the theoretical analysis and the generalization capability of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge