First-Order Preconditioning via Hypergradient Descent

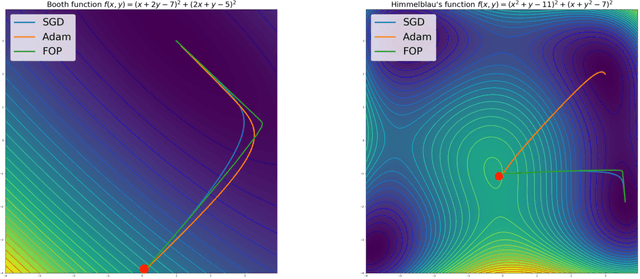
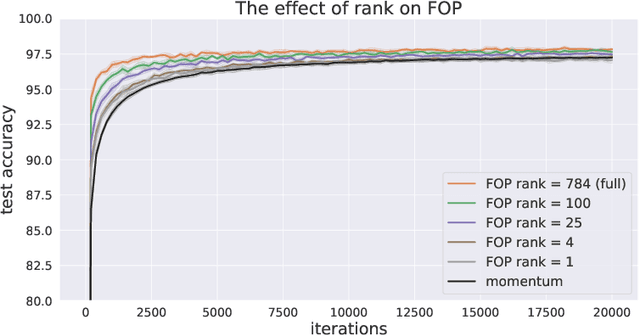
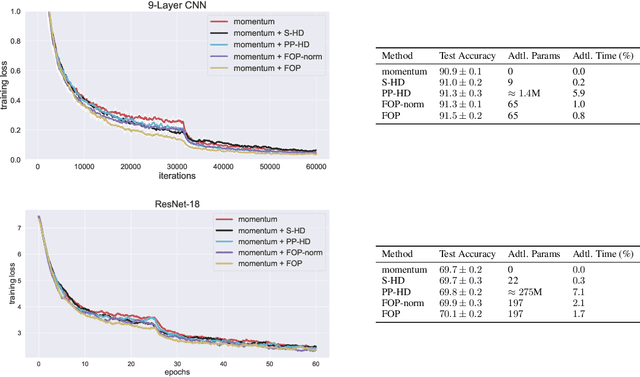
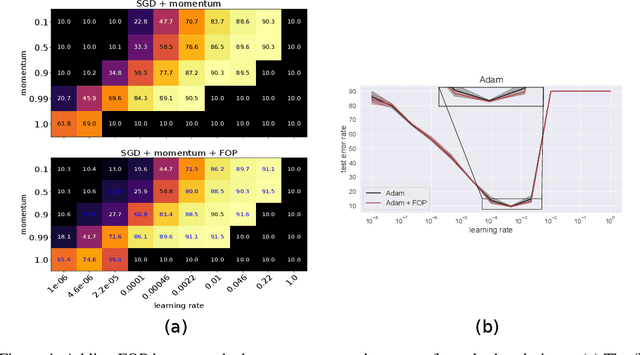
Standard gradient descent methods are susceptible to a range of issues that can impede training, such as high correlations and different scaling in parameter space. These difficulties can be addressed by second-order approaches that apply a preconditioning matrix to the gradient to improve convergence. Unfortunately, such algorithms typically struggle to scale to high-dimensional problems, in part because the calculation of specific preconditioners such as the inverse Hessian or Fisher information matrix is highly expensive. We introduce first-order preconditioning (FOP), a fast, scalable approach that generalizes previous work on hypergradient descent (Almeida et al., 1998; Maclaurin et al., 2015; Baydin et al., 2017) to learn a preconditioning matrix that only makes use of first-order information. Experiments show that FOP is able to improve the performance of standard deep learning optimizers on several visual classification tasks with minimal computational overhead. We also investigate the properties of the learned preconditioning matrices and perform a preliminary theoretical analysis of the algorithm.