Finding Regularized Competitive Equilibria of Heterogeneous Agent Macroeconomic Models with Reinforcement Learning
Paper and Code
Feb 24, 2023
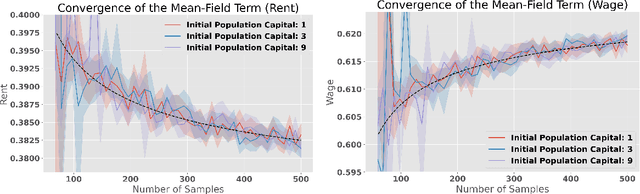
We study a heterogeneous agent macroeconomic model with an infinite number of households and firms competing in a labor market. Each household earns income and engages in consumption at each time step while aiming to maximize a concave utility subject to the underlying market conditions. The households aim to find the optimal saving strategy that maximizes their discounted cumulative utility given the market condition, while the firms determine the market conditions through maximizing corporate profit based on the household population behavior. The model captures a wide range of applications in macroeconomic studies, and we propose a data-driven reinforcement learning framework that finds the regularized competitive equilibrium of the model. The proposed algorithm enjoys theoretical guarantees in converging to the equilibrium of the market at a sub-linear rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge