Federated Survival Analysis with Discrete-Time Cox Models
Paper and Code
Jun 16, 2020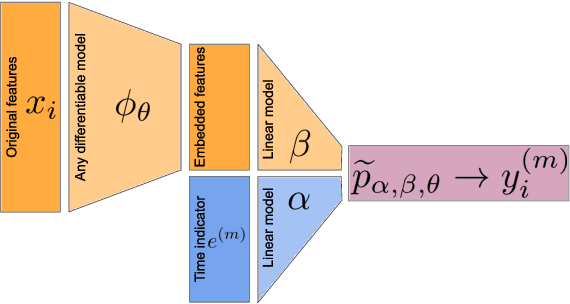
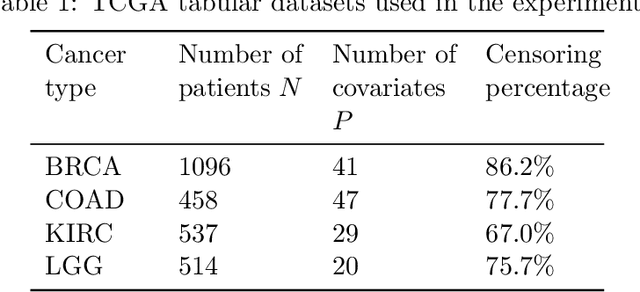
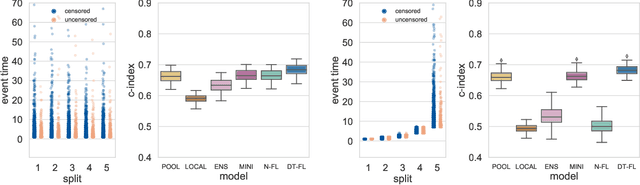
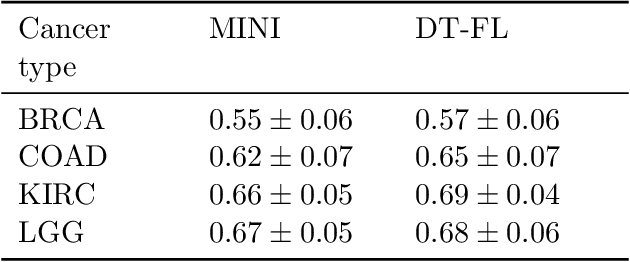
Building machine learning models from decentralized datasets located in different centers with federated learning (FL) is a promising approach to circumvent local data scarcity while preserving privacy. However, the prominent Cox proportional hazards (PH) model, used for survival analysis, does not fit the FL framework, as its loss function is non-separable with respect to the samples. The na\"ive method to bypass this non-separability consists in calculating the losses per center, and minimizing their sum as an approximation of the true loss. We show that the resulting model may suffer from important performance loss in some adverse settings. Instead, we leverage the discrete-time extension of the Cox PH model to formulate survival analysis as a classification problem with a separable loss function. Using this approach, we train survival models using standard FL techniques on synthetic data, as well as real-world datasets from The Cancer Genome Atlas (TCGA), showing similar performance to a Cox PH model trained on aggregated data. Compared to previous works, the proposed method is more communication-efficient, more generic, and more amenable to using privacy-preserving techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge