Fault Tolerance in Iterative-Convergent Machine Learning
Paper and Code
Oct 17, 2018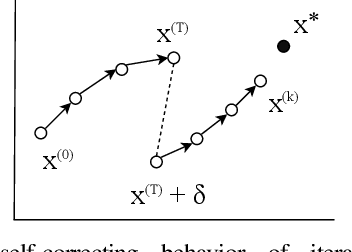
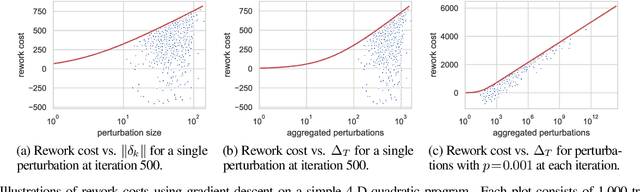
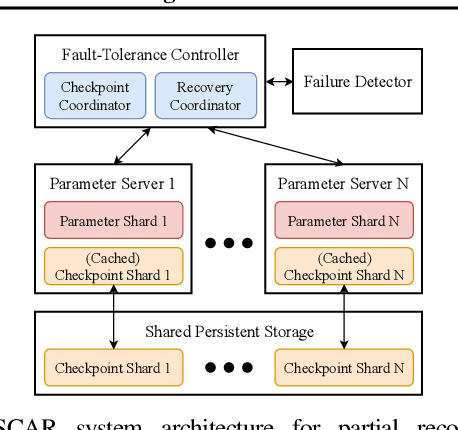
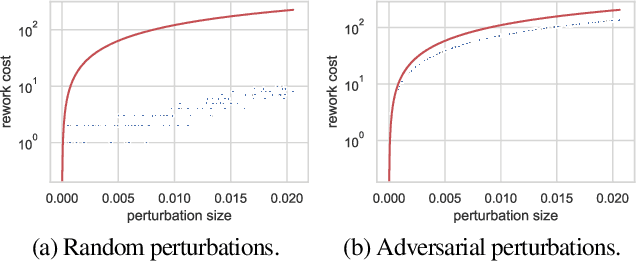
Machine learning (ML) training algorithms often possess an inherent self-correcting behavior due to their iterative-convergent nature. Recent systems exploit this property to achieve adaptability and efficiency in unreliable computing environments by relaxing the consistency of execution and allowing calculation errors to be self-corrected during training. However, the behavior of such systems are only well understood for specific types of calculation errors, such as those caused by staleness, reduced precision, or asynchronicity, and for specific types of training algorithms, such as stochastic gradient descent. In this paper, we develop a general framework to quantify the effects of calculation errors on iterative-convergent algorithms and use this framework to design new strategies for checkpoint-based fault tolerance. Our framework yields a worst-case upper bound on the iteration cost of arbitrary perturbations to model parameters during training. Our system, SCAR, employs strategies which reduce the iteration cost upper bound due to perturbations incurred when recovering from checkpoints. We show that SCAR can reduce the iteration cost of partial failures by 78% - 95% when compared with traditional checkpoint-based fault tolerance across a variety of ML models and training algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge