Fast Reinforcement Learning for Anti-jamming Communications
Paper and Code
Feb 13, 2020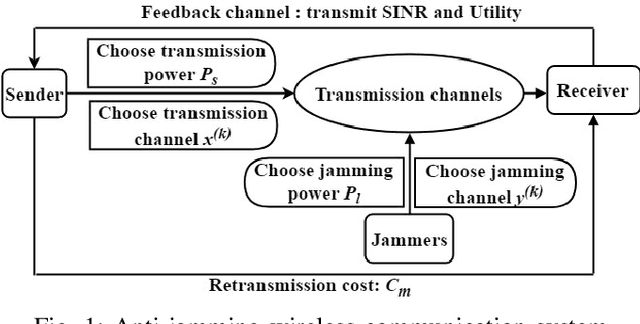

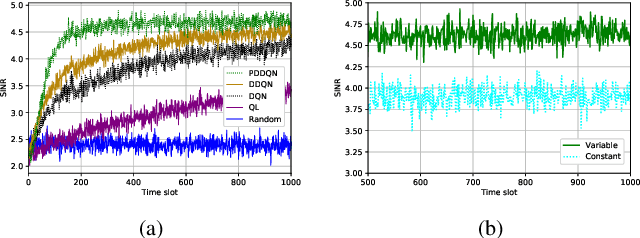
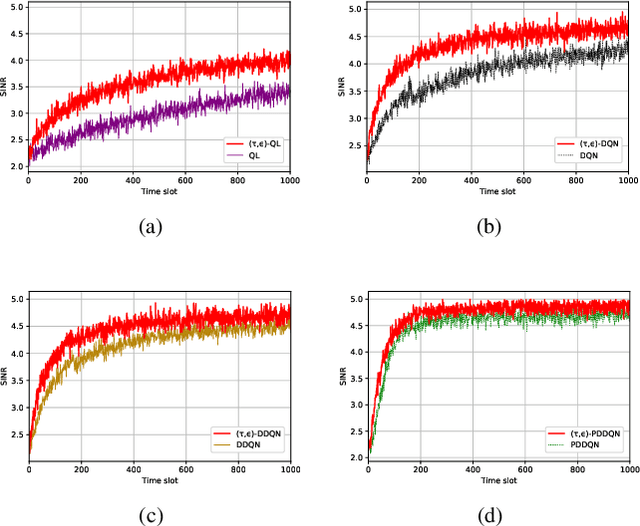
This letter presents a fast reinforcement learning algorithm for anti-jamming communications which chooses previous action with probability $\tau$ and applies $\epsilon$-greedy with probability $(1-\tau)$. A dynamic threshold based on the average value of previous several actions is designed and probability $\tau$ is formulated as a Gaussian-like function to guide the wireless devices. As a concrete example, the proposed algorithm is implemented in a wireless communication system against multiple jammers. Experimental results demonstrate that the proposed algorithm exceeds Q-learing, deep Q-networks (DQN), double DQN (DDQN), and prioritized experience reply based DDQN (PDDQN), in terms of signal-to-interference-plus-noise ratio and convergence rate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge