Fairness-Aware Neural Réyni Minimization for Continuous Features

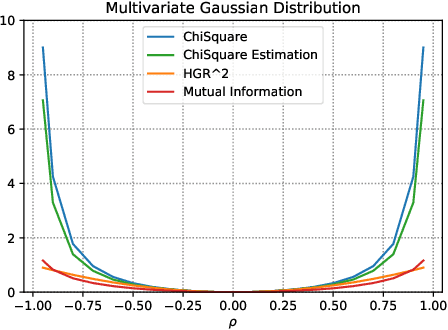
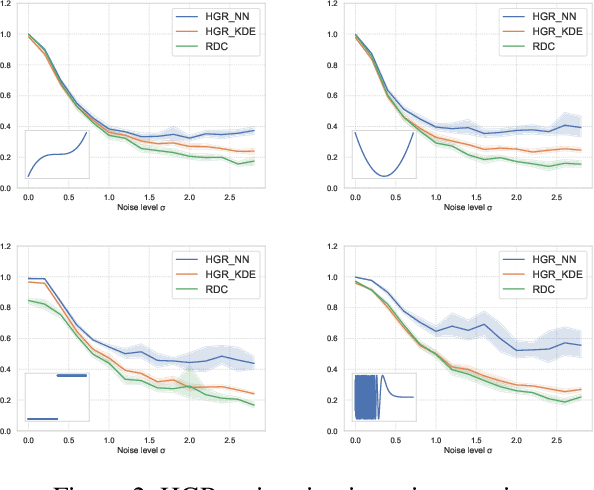
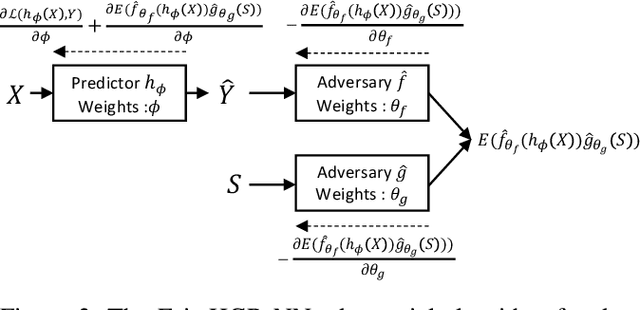
The past few years have seen a dramatic rise of academic and societal interest in fair machine learning. While plenty of fair algorithms have been proposed recently to tackle this challenge for discrete variables, only a few ideas exist for continuous ones. The objective in this paper is to ensure some independence level between the outputs of regression models and any given continuous sensitive variables. For this purpose, we use the Hirschfeld-Gebelein-R\'enyi (HGR) maximal correlation coefficient as a fairness metric. We propose two approaches to minimize the HGR coefficient. First, by reducing an upper bound of the HGR with a neural network estimation of the $\chi^{2}$ divergence. Second, by minimizing the HGR directly with an adversarial neural network architecture. The idea is to predict the output Y while minimizing the ability of an adversarial neural network to find the estimated transformations which are required to predict the HGR coefficient. We empirically assess and compare our approaches and demonstrate significant improvements on previously presented work in the field.