Fair Robust Assignment using Redundancy
Paper and Code
Mar 05, 2021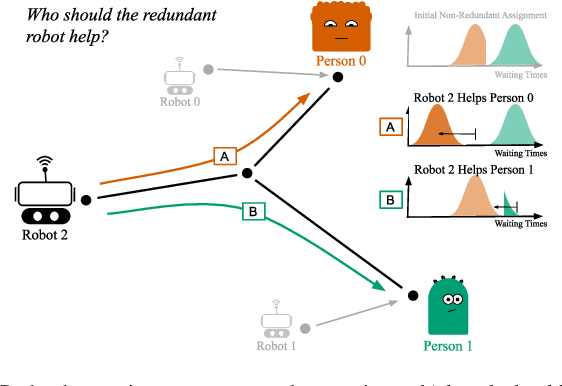
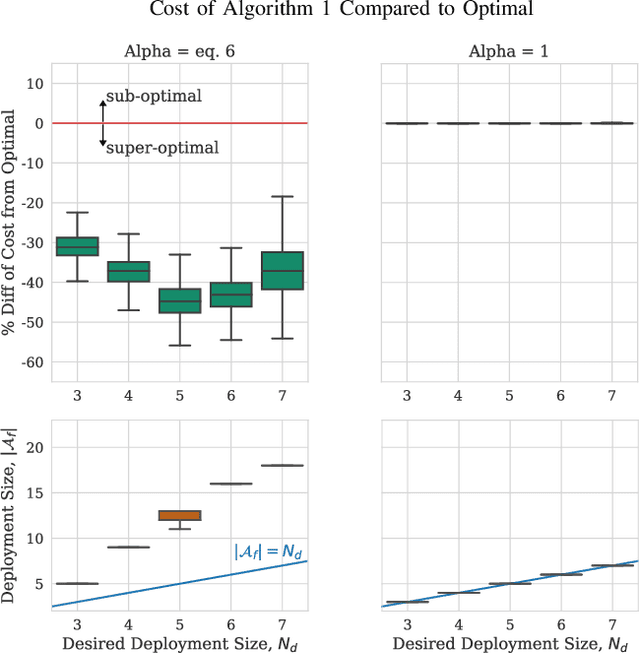
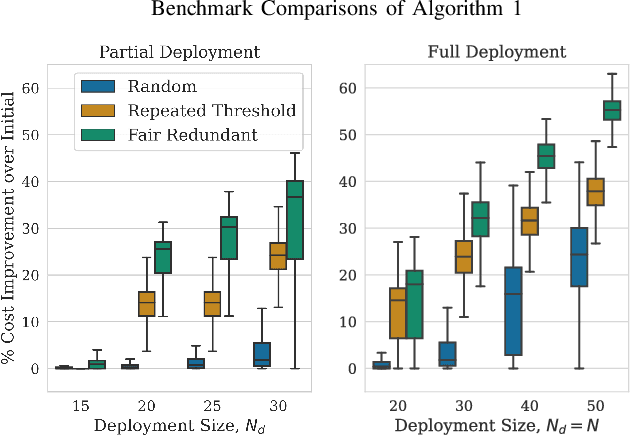
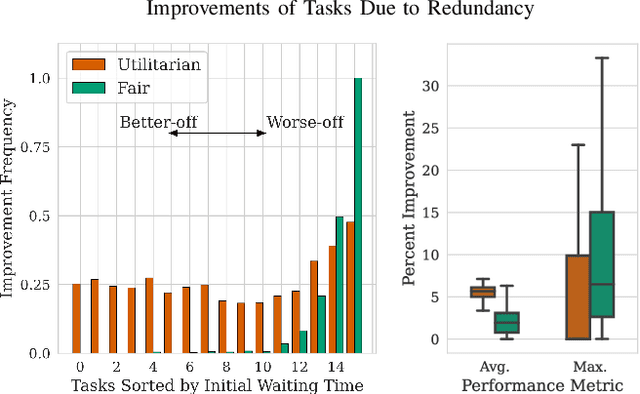
We study the consideration of fairness in redundant assignment for multi-agent task allocation. It has recently been shown that redundant assignment of agents to tasks provides robustness to uncertainty in task performance. However, the question of how to fairly assign these redundant resources across tasks remains unaddressed. In this paper, we present a novel problem formulation for fair redundant task allocation, which we cast as the optimization of worst-case task costs under a cardinality constraint. Solving this problem optimally is NP-hard. We exploit properties of supermodularity to propose a polynomial-time, near-optimal solution. In supermodular redundant assignment, the use of additional agents always improves task costs. Therefore, we provide a solution set that is $\alpha$ times larger than the cardinality constraint. This constraint relaxation enables our approach to achieve a super-optimal cost by using a sub-optimal assignment size. We derive the sub-optimality bound on this cardinality relaxation, $\alpha$. Additionally, we demonstrate that our algorithm performs near-optimally without the cardinality relaxation. We show simulations of redundant assignments of robots to goal nodes on transport networks with uncertain travel times. Empirically, our algorithm outperforms benchmarks, scales to large problems, and provides improvements in both fairness and average utility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge