Exploratory Landscape Analysis is Strongly Sensitive to the Sampling Strategy
Paper and Code
Jun 19, 2020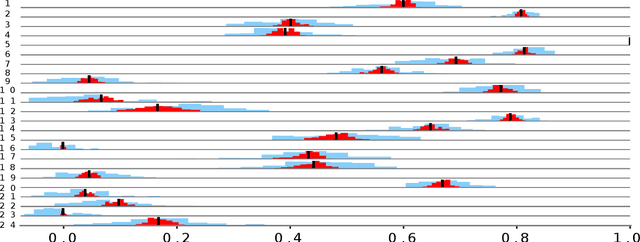
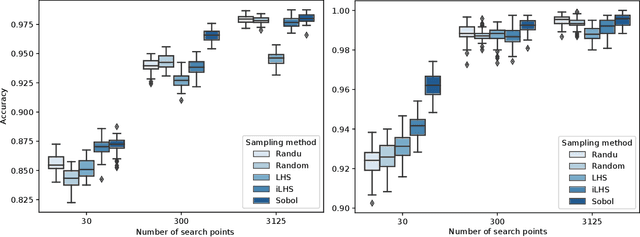
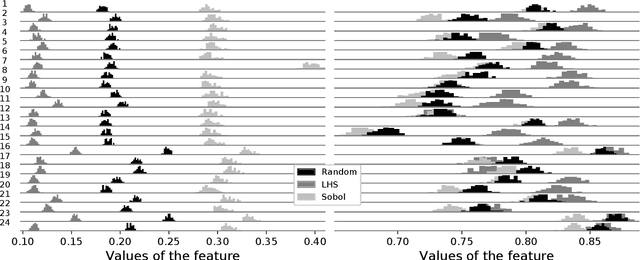
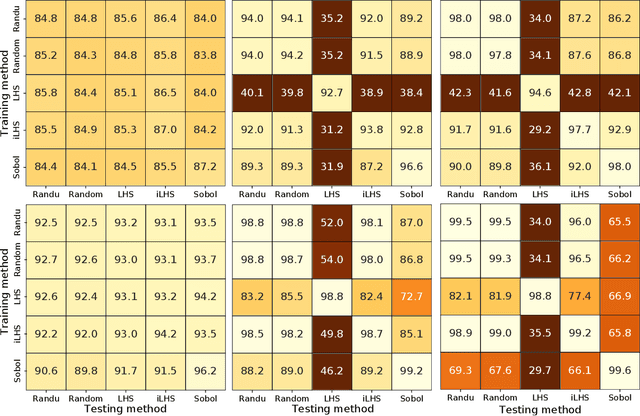
Exploratory landscape analysis (ELA) supports supervised learning approaches for automated algorithm selection and configuration by providing sets of features that quantify the most relevant characteristics of the optimization problem at hand. In black-box optimization, where an explicit problem representation is not available, the feature values need to be approximated from a small number of sample points. In practice, uniformly sampled random point sets and Latin hypercube constructions are commonly used sampling strategies. In this work, we analyze how the sampling method and the sample size influence the quality of the feature value approximations and how this quality impacts the accuracy of a standard classification task. While, not unexpectedly, increasing the number of sample points gives more robust estimates for the feature values, to our surprise we find that the feature value approximations for different sampling strategies do not converge to the same value. This implies that approximated feature values cannot be interpreted independently of the underlying sampling strategy. As our classification experiments show, this also implies that the feature approximations used for training a classifier must stem from the same sampling strategy as those used for the actual classification tasks. As a side result we show that classifiers trained with feature values approximated by Sobol' sequences achieve higher accuracy than any of the standard sampling techniques. This may indicate improvement potential for ELA-trained machine learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge