Evolved Policy Gradients
Paper and Code
Apr 29, 2018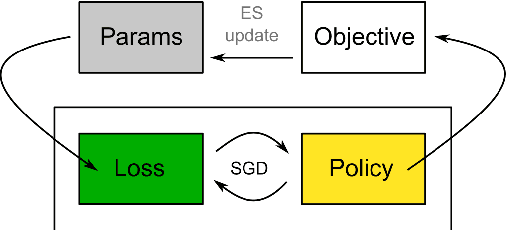

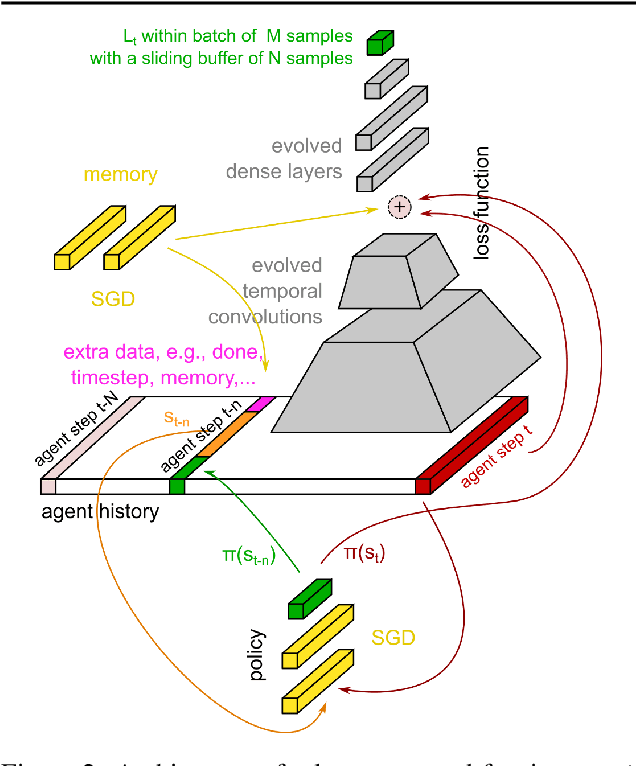

We propose a metalearning approach for learning gradient-based reinforcement learning (RL) algorithms. The idea is to evolve a differentiable loss function, such that an agent, which optimizes its policy to minimize this loss, will achieve high rewards. The loss is parametrized via temporal convolutions over the agent's experience. Because this loss is highly flexible in its ability to take into account the agent's history, it enables fast task learning. Empirical results show that our evolved policy gradient algorithm (EPG) achieves faster learning on several randomized environments compared to an off-the-shelf policy gradient method. We also demonstrate that EPG's learned loss can generalize to out-of-distribution test time tasks, and exhibits qualitatively different behavior from other popular metalearning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge