EvenNet: Ignoring Odd-Hop Neighbors Improves Robustness of Graph Neural Networks
Paper and Code
May 27, 2022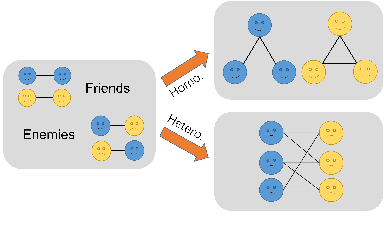
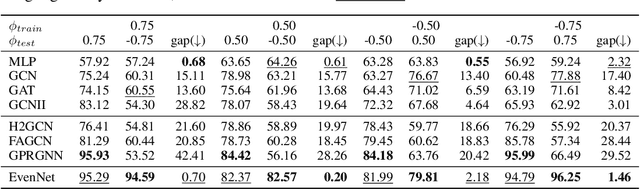
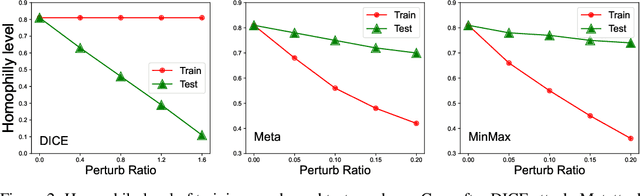
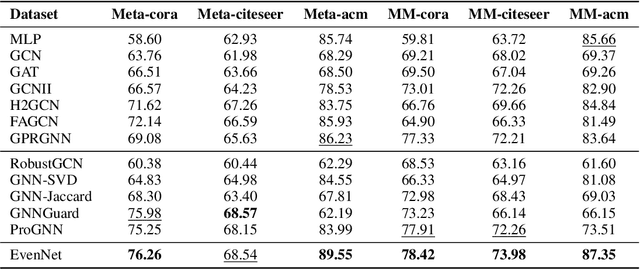
Graph Neural Networks (GNNs) have received extensive research attention for their promising performance in graph machine learning. Despite their extraordinary predictive accuracy, existing approaches, such as GCN and GPRGNN, are not robust in the face of homophily changes on test graphs, rendering these models vulnerable to graph structural attacks and with limited capacity in generalizing to graphs of varied homophily levels. Although many methods have been proposed to improve the robustness of GNN models, most of these techniques are restricted to the spatial domain and employ complicated defense mechanisms, such as learning new graph structures or calculating edge attentions. In this paper, we study the problem of designing simple and robust GNN models in the spectral domain. We propose EvenNet, a spectral GNN corresponding to an even-polynomial graph filter. Based on our theoretical analysis in both spatial and spectral domains, we demonstrate that EvenNet outperforms full-order models in generalizing across homophilic and heterophilic graphs, implying that ignoring odd-hop neighbors improves the robustness of GNNs. We conduct experiments on both synthetic and real-world datasets to demonstrate the effectiveness of EvenNet. Notably, EvenNet outperforms existing defense models against structural attacks without introducing additional computational costs and maintains competitiveness in traditional node classification tasks on homophilic and heterophilic graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge