Estimating g-Leakage via Machine Learning
Paper and Code
May 09, 2020
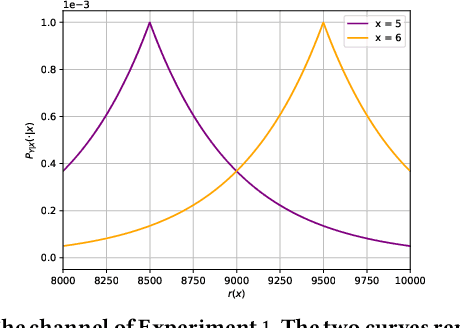
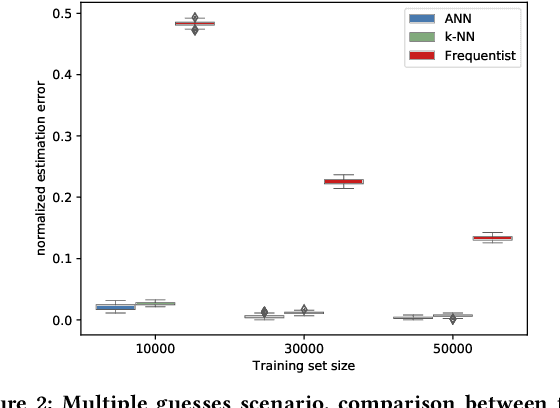
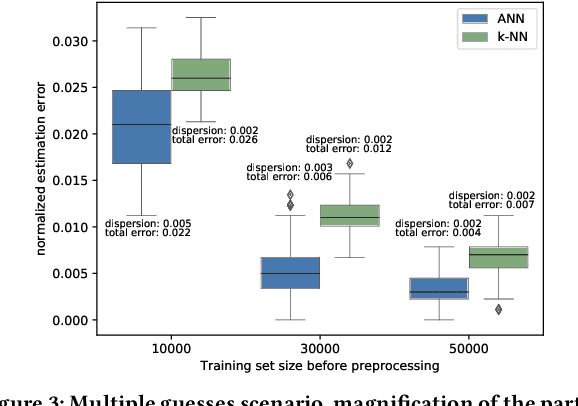
This paper considers the problem of estimating the information leakage of a system in the black-box scenario. It is assumed that the system's internals are unknown to the learner, or anyway too complicated to analyze, and the only available information are pairs of input-output data samples, possibly obtained by submitting queries to the system or provided by a third party. Previous research has mainly focused on counting the frequencies to estimate the input-output conditional probabilities (referred to as frequentist approach), however this method is not accurate when the domain of possible outputs is large. To overcome this difficulty, the estimation of the Bayes error of the ideal classifier was recently investigated using Machine Learning (ML) models and it has been shown to be more accurate thanks to the ability of those models to learn the input-output correspondence. However, the Bayes vulnerability is only suitable to describe one-try attacks. A more general and flexible measure of leakage is the g-vulnerability, which encompasses several different types of adversaries, with different goals and capabilities. In this paper, we propose a novel approach to perform black-box estimation of the g-vulnerability using ML. A feature of our approach is that it does not require to estimate the conditional probabilities, and that it is suitable for a large class of ML algorithms. First, we formally show the learnability for all data distributions. Then, we evaluate the performance via various experiments using k-Nearest Neighbors and Neural Networks. Our results outperform the frequentist approach when the observables domain is large.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge