ES-GNN: Generalizing Graph Neural Networks Beyond Homophily with Edge Splitting

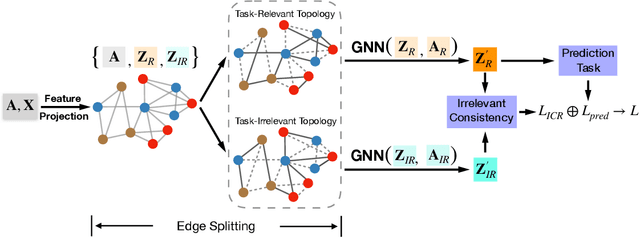
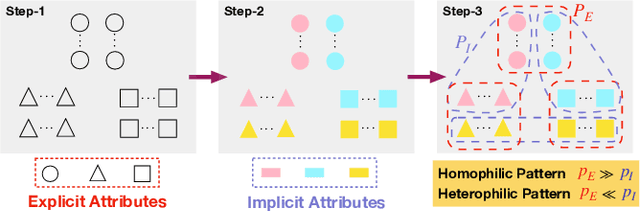
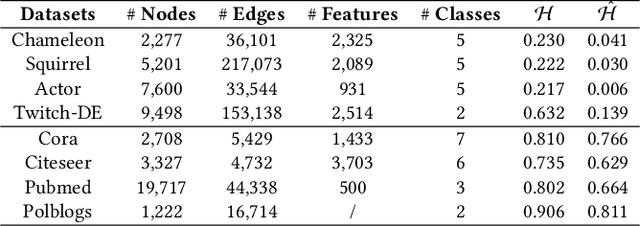
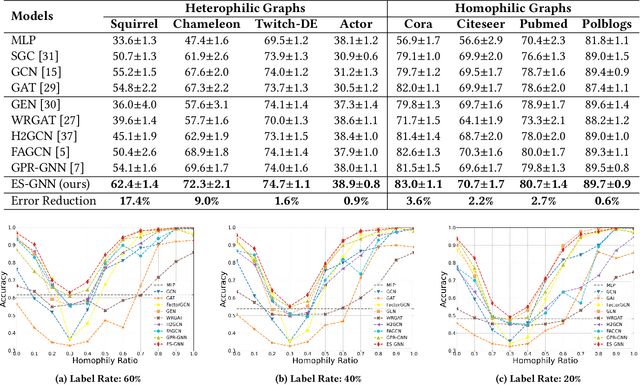
Graph Neural Networks (GNNs) have achieved enormous success in tackling analytical problems on graph data. Most GNNs interpret nearly all the node connections as inductive bias with feature smoothness, and implicitly assume strong homophily on the observed graph. However, real-world networks are not always homophilic, but sometimes exhibit heterophilic patterns where adjacent nodes share dissimilar attributes and distinct labels. Therefore,GNNs smoothing the node proximity holistically may aggregate inconsistent information arising from both task-relevant and irrelevant connections. In this paper, we propose a novel edge splitting GNN (ES-GNN) framework, which generalizes GNNs beyond homophily by jointly partitioning network topology and disentangling node features. Specifically, the proposed framework employs an interpretable operation to adaptively split the set of edges of the original graph into two exclusive sets indicating respectively the task-relevant and irrelevant relations among nodes. The node features are then aggregated separately on these two partial edge sets to produce disentangled representations, based on which a more accurate edge splitting can be attained later. Theoretically, we show that our ES-GNN can be regarded as a solution to a graph denoising problem with a disentangled smoothness assumption, which further illustrates our motivations and interprets the improved generalization. Extensive experiments over 8 benchmark and 1 synthetic datasets demonstrate that ES-GNN not only outperforms the state-of-the-arts (including 8 GNN baselines), but also can be more robust to adversarial graphs and alleviate the over-smoothing problem.