Enhancing Reinforcement Learning in Sensor Fusion: A Comparative Analysis of Cubature and Sampling-based Integration Methods for Rover Search Planning
Paper and Code
May 15, 2024
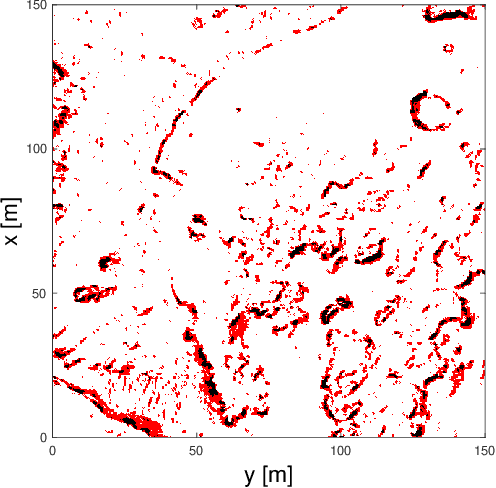
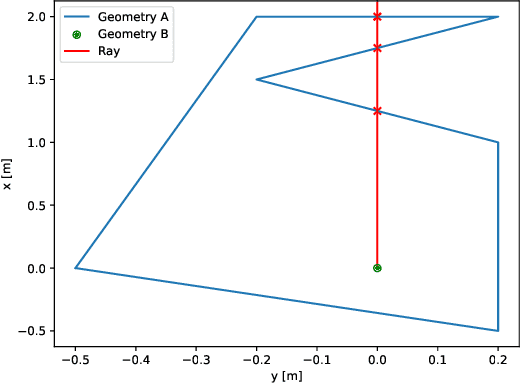
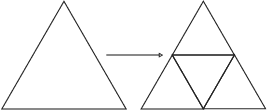
This study investigates the computational speed and accuracy of two numerical integration methods, cubature and sampling-based, for integrating an integrand over a 2D polygon. Using a group of rovers searching the Martian surface with a limited sensor footprint as a test bed, the relative error and computational time are compared as the area was subdivided to improve accuracy in the sampling-based approach. The results show that the sampling-based approach exhibits a $14.75\%$ deviation in relative error compared to cubature when it matches the computational performance at $100\%$. Furthermore, achieving a relative error below $1\%$ necessitates a $10000\%$ increase in relative time to calculate due to the $\mathcal{O}(N^2)$ complexity of the sampling-based method. It is concluded that for enhancing reinforcement learning capabilities and other high iteration algorithms, the cubature method is preferred over the sampling-based method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge