End-to-end Learning the Partial Permutation Matrix for Robust 3D Point Cloud Registration
Paper and Code
Oct 28, 2021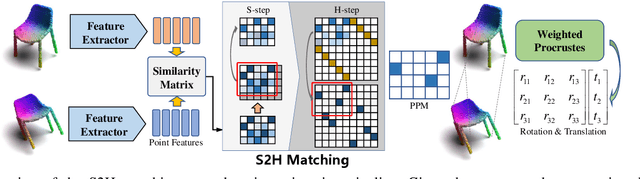
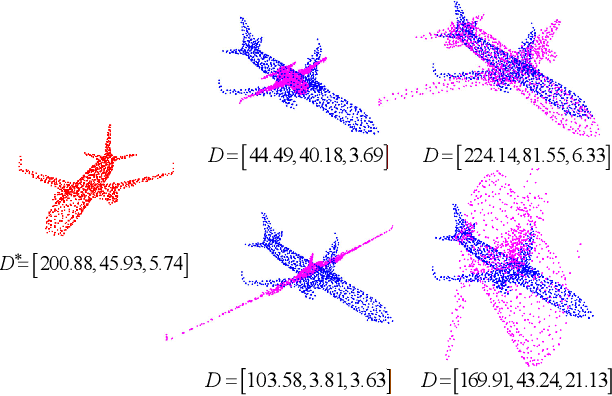
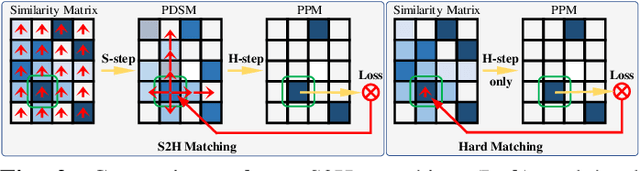
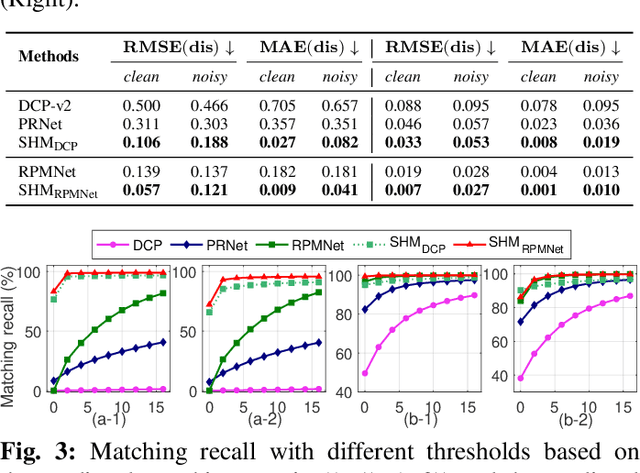
Even though considerable progress has been made in deep learning-based 3D point cloud processing, how to obtain accurate correspondences for robust registration remains a major challenge because existing hard assignment methods cannot deal with outliers naturally. Alternatively, the soft matching-based methods have been proposed to learn the matching probability rather than hard assignment. However, in this paper, we prove that these methods have an inherent ambiguity causing many deceptive correspondences. To address the above challenges, we propose to learn a partial permutation matching matrix, which does not assign corresponding points to outliers, and implements hard assignment to prevent ambiguity. However, this proposal poses two new problems, i.e., existing hard assignment algorithms can only solve a full rank permutation matrix rather than a partial permutation matrix, and this desired matrix is defined in the discrete space, which is non-differentiable. In response, we design a dedicated soft-to-hard (S2H) matching procedure within the registration pipeline consisting of two steps: solving the soft matching matrix (S-step) and projecting this soft matrix to the partial permutation matrix (H-step). Specifically, we augment the profit matrix before the hard assignment to solve an augmented permutation matrix, which is cropped to achieve the final partial permutation matrix. Moreover, to guarantee end-to-end learning, we supervise the learned partial permutation matrix but propagate the gradient to the soft matrix instead. Our S2H matching procedure can be easily integrated with existing registration frameworks, which has been verified in representative frameworks including DCP, RPMNet, and DGR. Extensive experiments have validated our method, which creates a new state-of-the-art performance for robust 3D point cloud registration. The code will be made public.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge