Encoding Invariances in Deep Generative Models
Paper and Code
Jun 04, 2019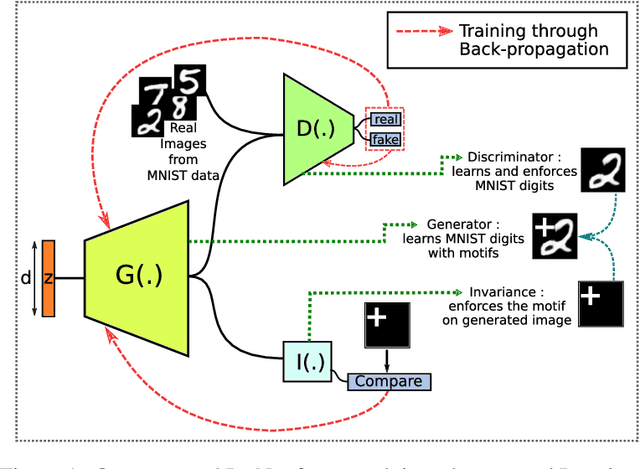
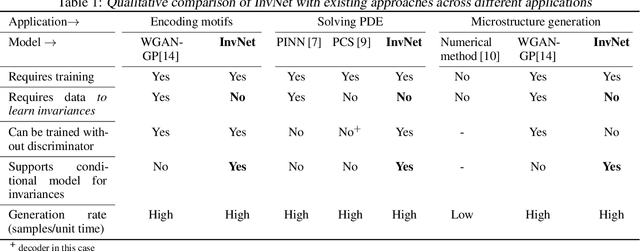
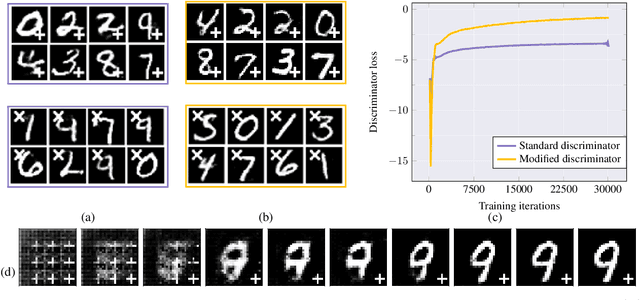
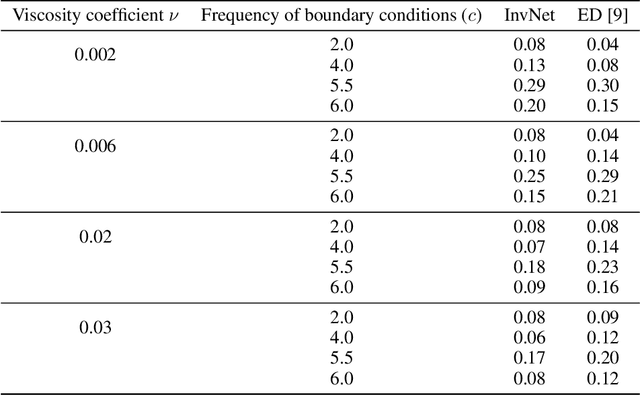
Reliable training of generative adversarial networks (GANs) typically require massive datasets in order to model complicated distributions. However, in several applications, training samples obey invariances that are \textit{a priori} known; for example, in complex physics simulations, the training data obey universal laws encoded as well-defined mathematical equations. In this paper, we propose a new generative modeling approach, InvNet, that can efficiently model data spaces with known invariances. We devise an adversarial training algorithm to encode them into data distribution. We validate our framework in three experimental settings: generating images with fixed motifs; solving nonlinear partial differential equations (PDEs); and reconstructing two-phase microstructures with desired statistical properties. We complement our experiments with several theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge