Enabling Robust State Estimation through Measurement Error Covariance Adaptation

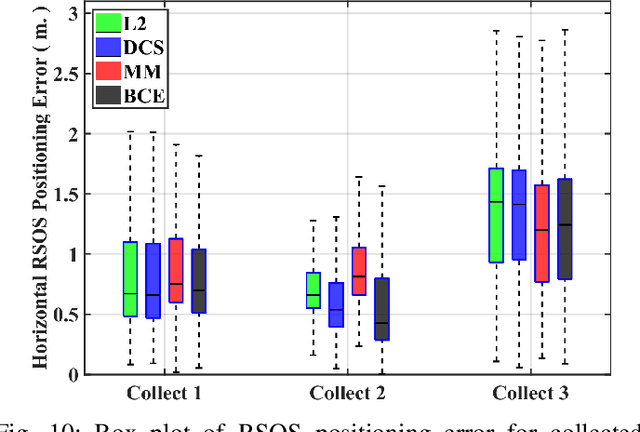
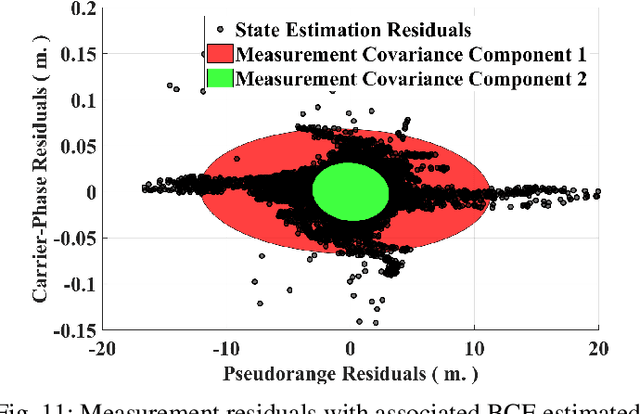
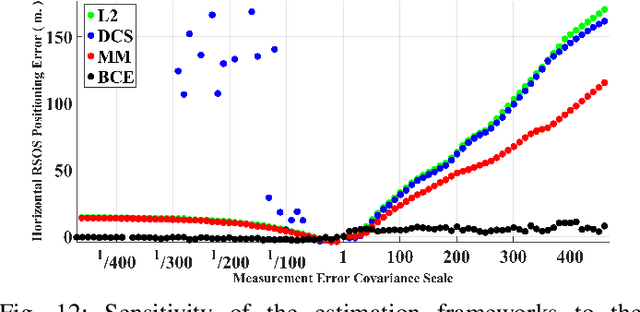
Accurate platform localization is an integral component of most robotic systems. As these robotic systems become more ubiquitous, it is necessary to develop robust state estimation algorithms that are able to withstand novel and non-cooperative environments. When dealing with novel and non-cooperative environments, little is known a priori about the measurement error uncertainty, thus, there is a requirement that the uncertainty models of the localization algorithm be adaptive. Within this paper, we propose one such technique that enables robust state estimation through the iterative adaptation of the measurement uncertainty model. The adaptation of the measurement uncertainty model is granted through non-parametric clustering of the residuals, which enables the characterization of the measurement uncertainty via a Gaussian mixture model. The provided Gaussian mixture model can be utilized within any non-linear least squares optimization algorithm by approximately characterizing each observation with the sufficient statistics of the assigned cluster (i.e., each observation's uncertainty model is updated based upon the assignment provided by the non-parametric clustering algorithm). The proposed algorithm is verified on several GNSS collected data sets, where it is shown that the proposed technique exhibits some advantages when compared to other robust estimation techniques when confronted with degraded data quality.