Elastically-Constrained Meta-Learner for Federated Learning
Paper and Code
Jun 30, 2023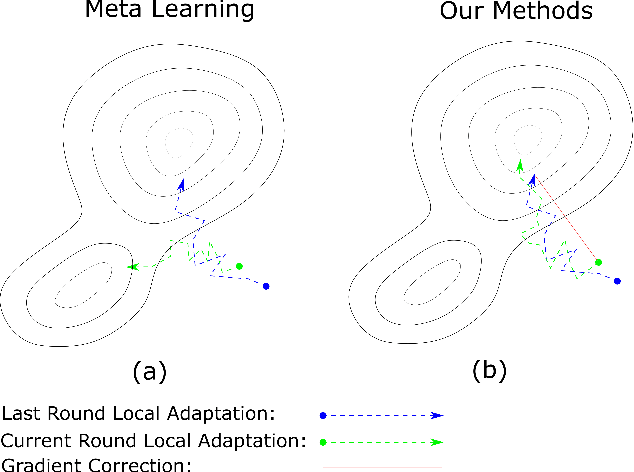
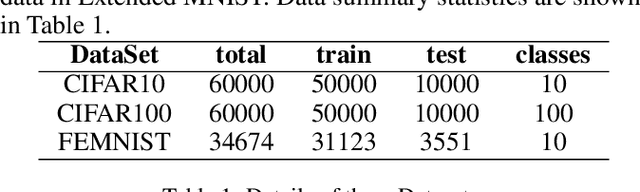
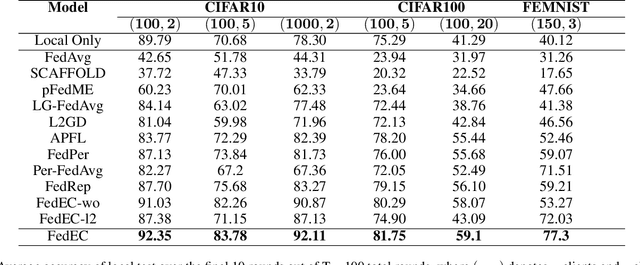
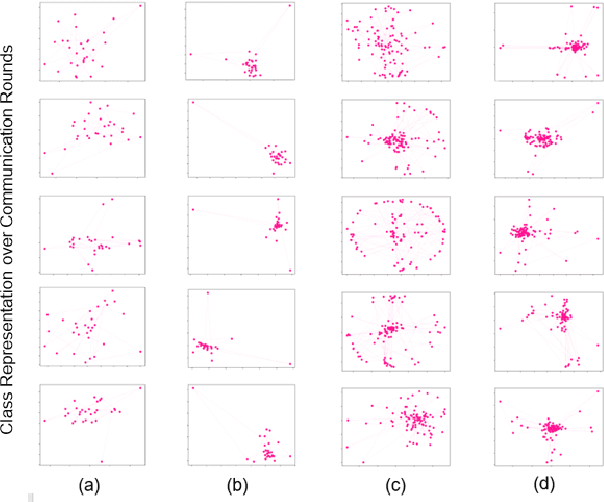
Federated learning is an approach to collaboratively training machine learning models for multiple parties that prohibit data sharing. One of the challenges in federated learning is non-IID data between clients, as a single model can not fit the data distribution for all clients. Meta-learning, such as Per-FedAvg, is introduced to cope with the challenge. Meta-learning learns shared initial parameters for all clients. Each client employs gradient descent to adapt the initialization to local data distributions quickly to realize model personalization. However, due to non-convex loss function and randomness of sampling update, meta-learning approaches have unstable goals in local adaptation for the same client. This fluctuation in different adaptation directions hinders the convergence in meta-learning. To overcome this challenge, we use the historical local adapted model to restrict the direction of the inner loop and propose an elastic-constrained method. As a result, the current round inner loop keeps historical goals and adapts to better solutions. Experiments show our method boosts meta-learning convergence and improves personalization without additional calculation and communication. Our method achieved SOTA on all metrics in three public datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge