Elastic Similarity Measures for Multivariate Time Series Classification

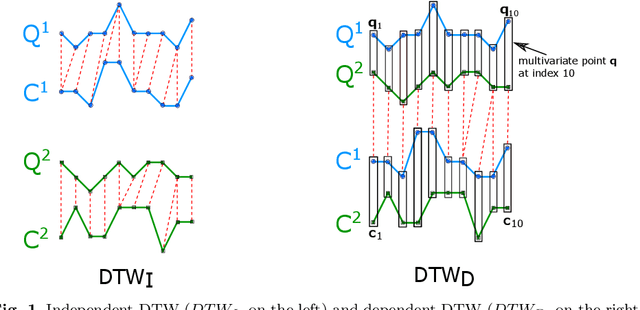
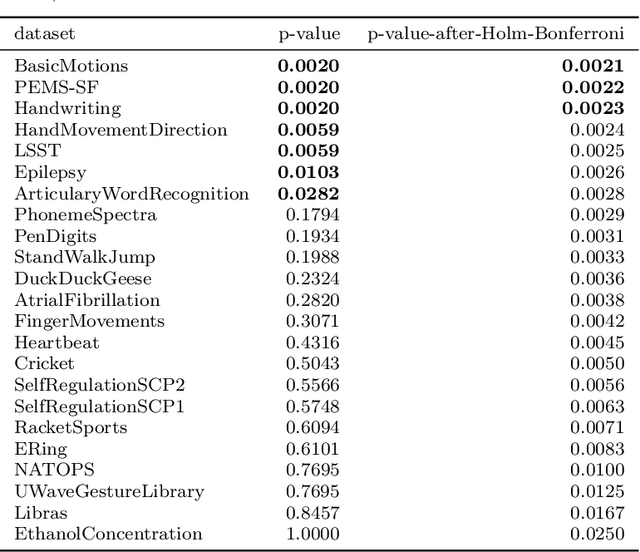
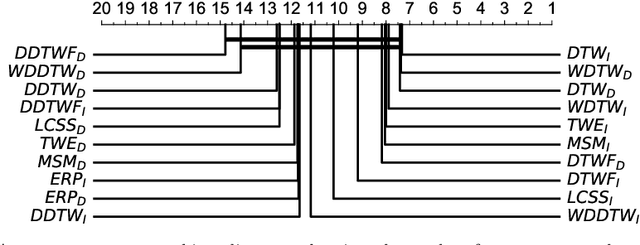
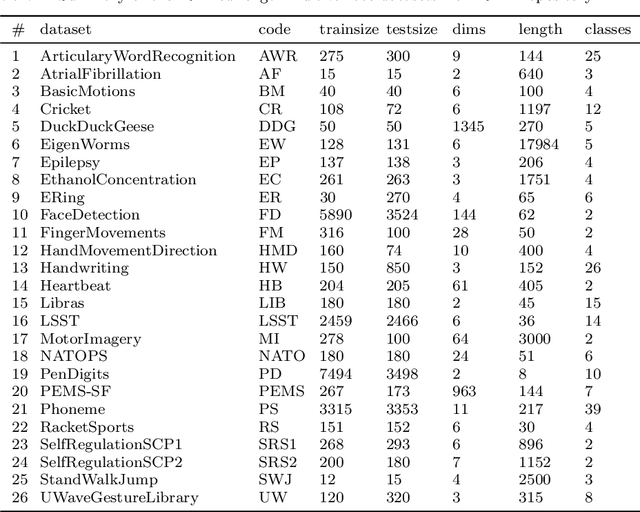
Elastic similarity measures are a class of similarity measures specifically designed to work with time series data. When scoring the similarity between two time series, they allow points that do not correspond in timestamps to be aligned. This can compensate for misalignments in the time axis of time series data, and for similar processes that proceed at variable and differing paces. Elastic similarity measures are widely used in machine learning tasks such as classification, clustering and outlier detection when using time series data. There is a multitude of research on various univariate elastic similarity measures. However, except for multivariate versions of the well known Dynamic Time Warping (DTW) there is a lack of work to generalise other similarity measures for multivariate cases. This paper adapts two existing strategies used in multivariate DTW, namely, Independent and Dependent DTW, to several commonly used elastic similarity measures. Using 23 datasets from the University of East Anglia (UEA) multivariate archive, for nearest neighbour classification, we demonstrate that each measure outperforms all others on at least one dataset and that there are datasets for which either the dependent versions of all measures are more accurate than their independent counterparts or vice versa. This latter finding suggests that these differences arise from a fundamental property of the data. We also show that an ensemble of such nearest neighbour classifiers is highly competitive with other state-of-the-art multivariate time series classifiers.