EIGNN: Efficient Infinite-Depth Graph Neural Networks
Paper and Code
Feb 22, 2022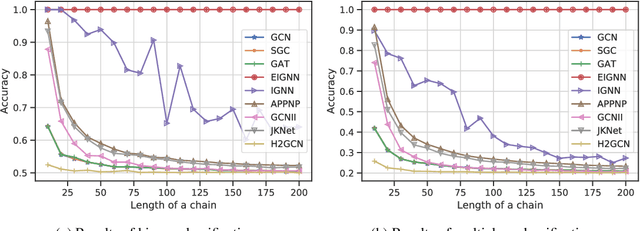
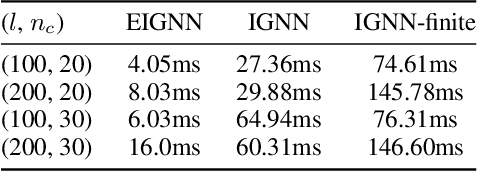
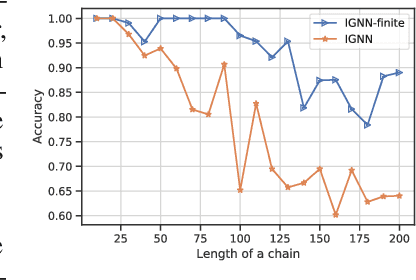
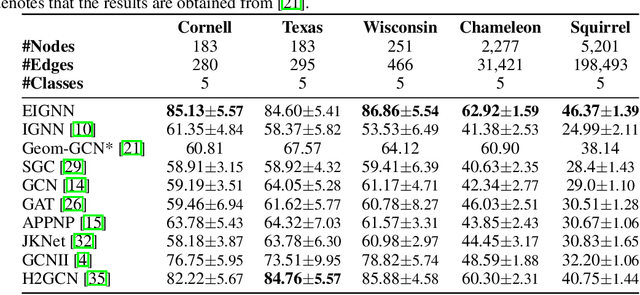
Graph neural networks (GNNs) are widely used for modelling graph-structured data in numerous applications. However, with their inherently finite aggregation layers, existing GNN models may not be able to effectively capture long-range dependencies in the underlying graphs. Motivated by this limitation, we propose a GNN model with infinite depth, which we call Efficient Infinite-Depth Graph Neural Networks (EIGNN), to efficiently capture very long-range dependencies. We theoretically derive a closed-form solution of EIGNN which makes training an infinite-depth GNN model tractable. We then further show that we can achieve more efficient computation for training EIGNN by using eigendecomposition. The empirical results of comprehensive experiments on synthetic and real-world datasets show that EIGNN has a better ability to capture long-range dependencies than recent baselines, and consistently achieves state-of-the-art performance. Furthermore, we show that our model is also more robust against both noise and adversarial perturbations on node features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge