Efficient Search of the k Shortest Non-Homotopic Paths by Eliminating Non-k-Optimal Topologies
Paper and Code
Jul 27, 2022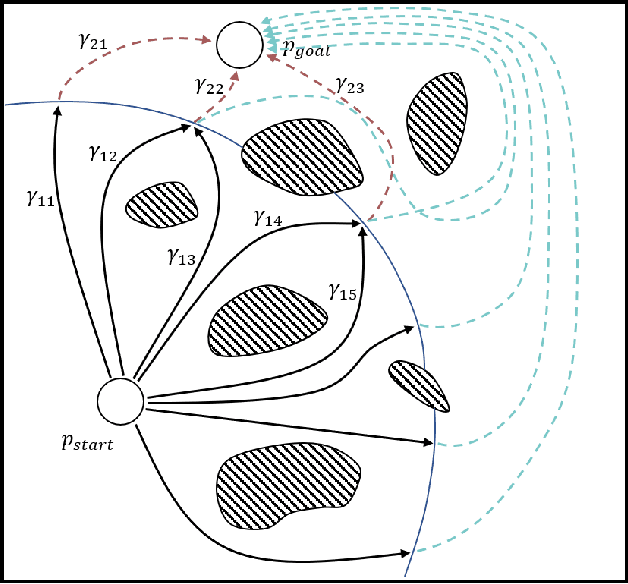


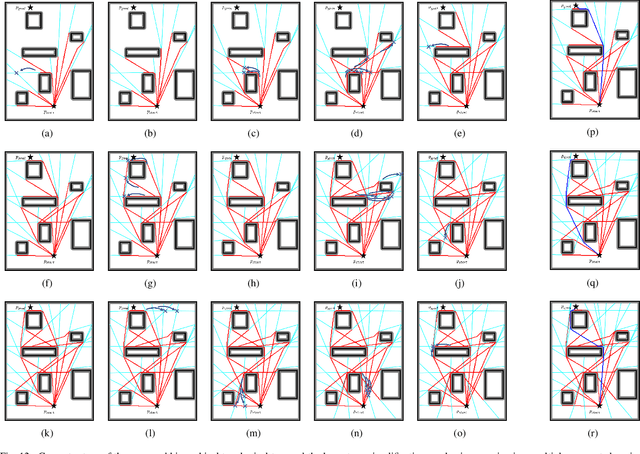
An efficient algorithm to solve the $k$ shortest non-homotopic path planning ($k$-SNPP) problem in a 2D environment is proposed in this paper. Motivated by accelerating the inefficient exploration of the homotopy-augmented space of the 2D environment, our fundamental idea is to identify the non-$k$-optimal path topologies as early as possible and terminate the pathfinding along them. This is a non-trivial practice because it has to be done at an intermediate state of the path planning process when locally shortest paths have not been fully constructed. In other words, the paths to be compared have not rendezvoused at the goal location, which makes the homotopy theory, modelling the spatial relationship among the paths having the same endpoint, not applicable. This paper is the first work that develops a systematic distance-based topology simplification mechanism to solve the $k$-SNPP task, whose core contribution is to assert the distance-based order of non-homotopic locally shortest paths before constructing them. If the order can be predicted, then those path topologies having more than $k$ better topologies are proven free of the desired $k$ paths and thus can be safely discarded during the path planning process. To this end, a hierarchical topological tree is proposed as an implementation of the mechanism, whose nodes are proven to expand in non-homotopic directions and edges (collision-free path segments) are proven locally shortest. With efficient criteria that observe the order relations between partly constructed locally shortest paths being imparted into the tree, the tree nodes that expand in non-$k$-optimal topologies will not be expanded. As a result, the computational time for solving the $k$-SNPP problem is reduced by near two orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge