Efficient Penetration Depth Computation between Rigid Models using Contact Space Propagation Sampling
Paper and Code
Nov 13, 2015

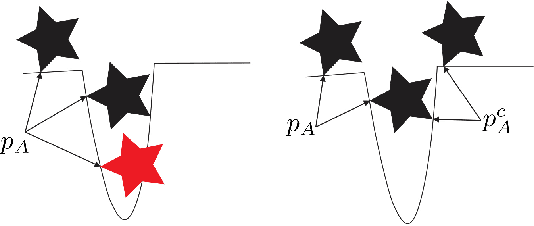

We present a novel method to compute the approximate global penetration depth (PD) between two non-convex geometric models. Our approach consists of two phases: offline precomputation and run-time queries. In the first phase, our formulation uses a novel sampling algorithm to precompute an approximation of the high-dimensional contact space between the pair of models. As compared with prior random sampling algorithms for contact space approximation, our propagation sampling considerably speeds up the precomputation and yields a high quality approximation. At run-time, we perform a nearest-neighbor query and local projection to efficiently compute the translational or generalized PD. We demonstrate the performance of our approach on complex 3D benchmarks with tens or hundreds of thousands of triangles, and we observe significant improvement over previous methods in terms of accuracy, with a modest improvement in the run-time performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge