Efficient Multi-Agent Motion Planning in Continuous Workspaces Using Medial-Axis-Based Swap Graphs

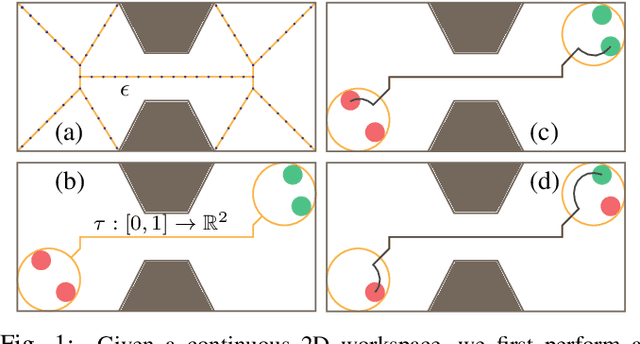
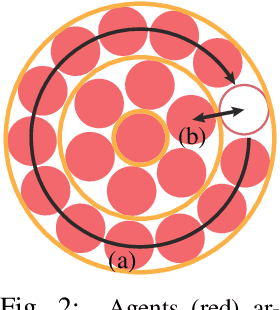
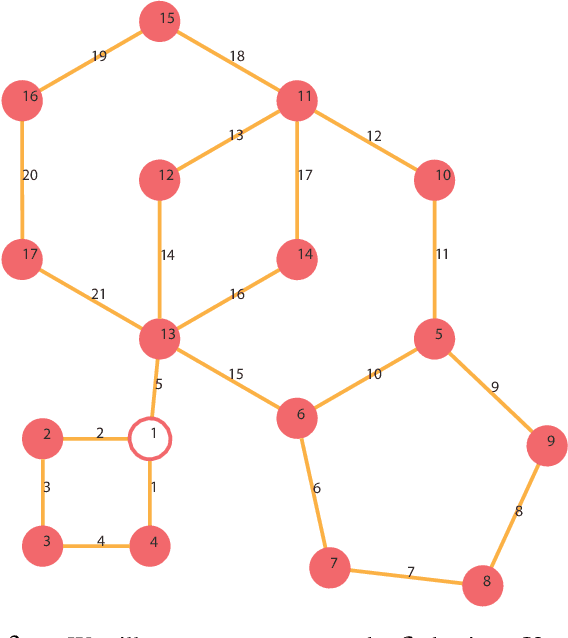
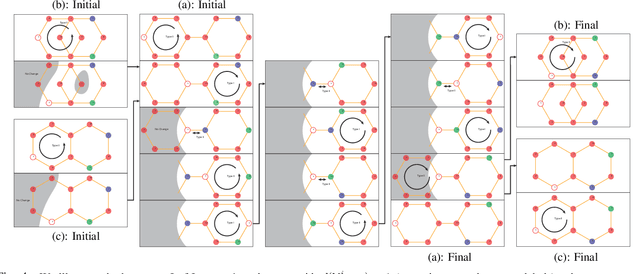
We present an algorithm for homogeneous, labeled, and disk-shaped multi-agent motion planning in continuous workspaces with arbitrarily-shaped obstacles. Our method consists of two steps. First, we convert the continuous free space into a discrete graph where agents are placed on vertices and move along edges. On the graph, a set of swap operations are defined and we ensure that performing these swap operations will not lead to collisions between agents or with obstacles. Second, we prove that it is possible for agents' locations to be arbitrarily permuted on graph vertices using our swap operations, as long as these graph vertices are not fully occupied. In other words, a multi-agent motion planning problem on our graph is always solvable. Finally, we show that such continuous-to-discrete conversion can be performed efficiently with the help of a medial axis analysis and can be performed robustly for workspaces with arbitrarily-shaped obstacles. Moreover, the resulting graph has many vertices and can accommodate a large number of densely packed agents (up to $69\%$ of the volume of free space), and motion plans can be computed $10\times$ faster using our swap operations compared to state-of-the-art methods.