Efficient Inference and Learning in a Large Knowledge Base: Reasoning with Extracted Information using a Locally Groundable First-Order Probabilistic Logic
Paper and Code
Apr 12, 2014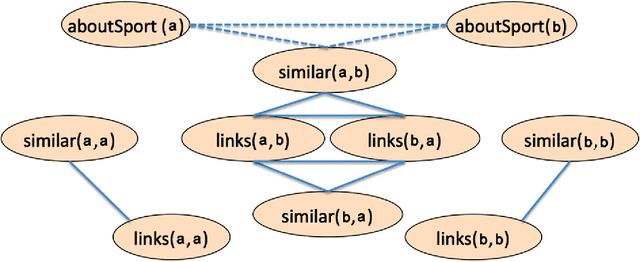

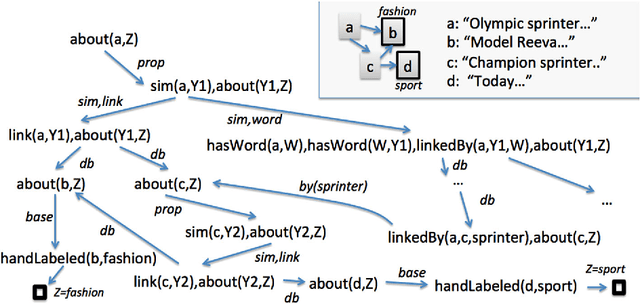

One important challenge for probabilistic logics is reasoning with very large knowledge bases (KBs) of imperfect information, such as those produced by modern web-scale information extraction systems. One scalability problem shared by many probabilistic logics is that answering queries involves "grounding" the query---i.e., mapping it to a propositional representation---and the size of a "grounding" grows with database size. To address this bottleneck, we present a first-order probabilistic language called ProPPR in which that approximate "local groundings" can be constructed in time independent of database size. Technically, ProPPR is an extension to stochastic logic programs (SLPs) that is biased towards short derivations; it is also closely related to an earlier relational learning algorithm called the path ranking algorithm (PRA). We show that the problem of constructing proofs for this logic is related to computation of personalized PageRank (PPR) on a linearized version of the proof space, and using on this connection, we develop a proveably-correct approximate grounding scheme, based on the PageRank-Nibble algorithm. Building on this, we develop a fast and easily-parallelized weight-learning algorithm for ProPPR. In experiments, we show that learning for ProPPR is orders magnitude faster than learning for Markov logic networks; that allowing mutual recursion (joint learning) in KB inference leads to improvements in performance; and that ProPPR can learn weights for a mutually recursive program with hundreds of clauses, which define scores of interrelated predicates, over a KB containing one million entities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge