Efficient Global Point Cloud Alignment using Bayesian Nonparametric Mixtures
Paper and Code
Nov 22, 2016
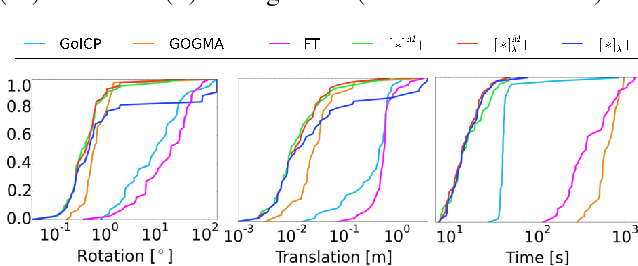
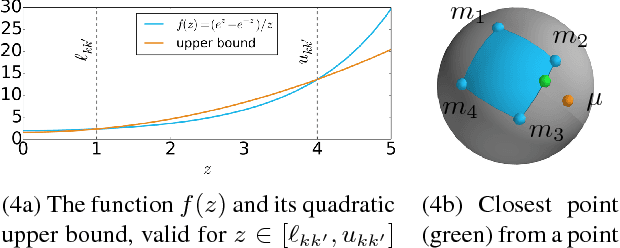
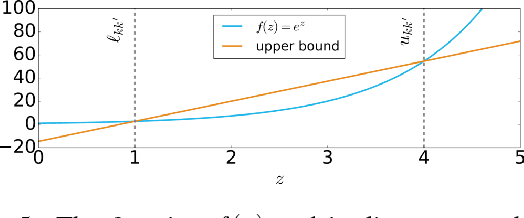
Point cloud alignment is a common problem in computer vision and robotics, with applications ranging from 3D object recognition to reconstruction. We propose a novel approach to the alignment problem that utilizes Bayesian nonparametrics to describe the point cloud and surface normal densities, and branch and bound (BB) optimization to recover the relative transformation. BB uses a novel, refinable, near-uniform tessellation of rotation space using 4D tetrahedra, leading to more efficient optimization compared to the common axis-angle tessellation. We provide objective function bounds for pruning given the proposed tessellation, and prove that BB converges to the optimum of the cost function along with providing its computational complexity. Finally, we empirically demonstrate the efficiency of the proposed approach as well as its robustness to real-world conditions such as missing data and partial overlap.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge