Dynamically Stable Poincaré Embeddings for Neural Manifolds

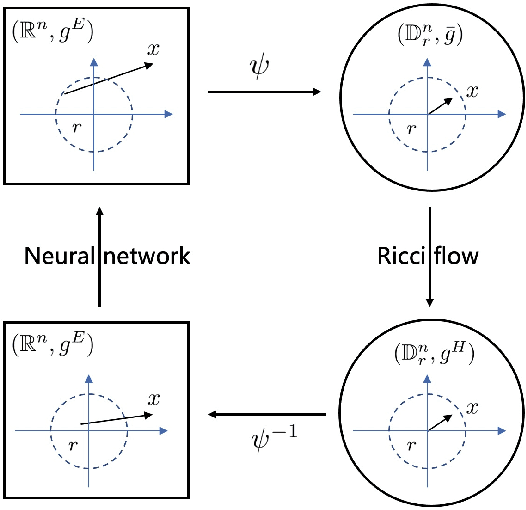
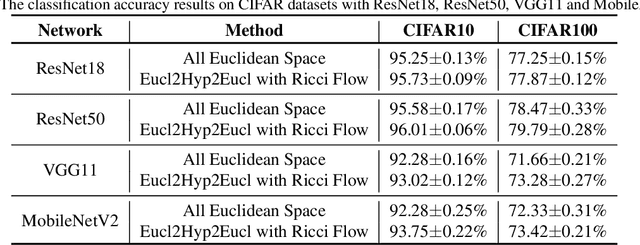
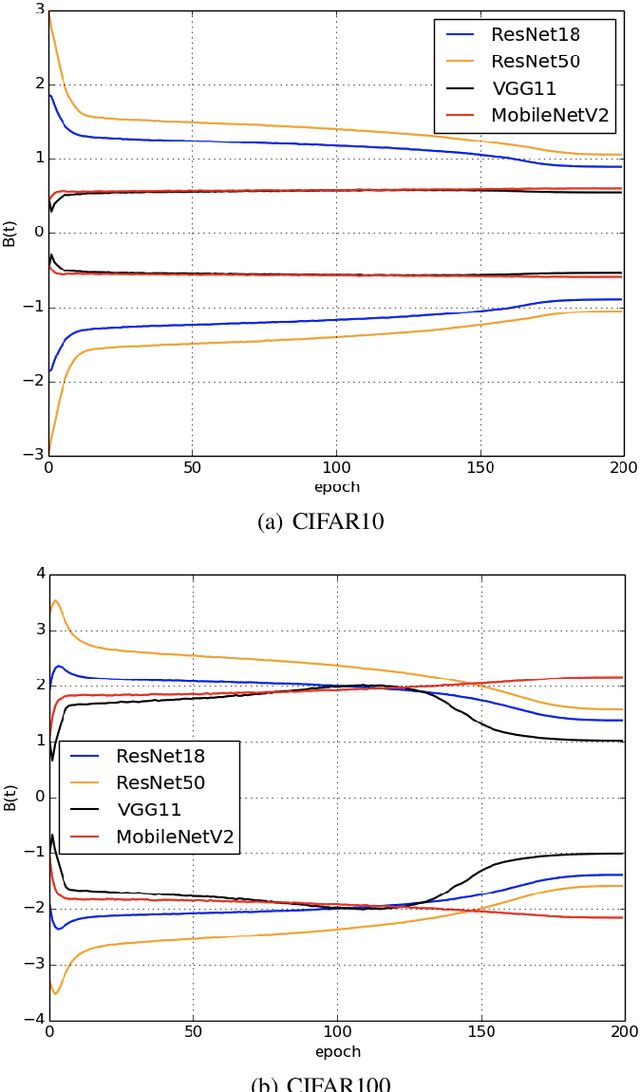
In a Riemannian manifold, the Ricci flow is a partial differential equation for evolving the metric to become more regular. We hope that topological structures from such metrics may be used to assist in the tasks of machine learning. However, this part of the work is still missing. In this paper, we bridge this gap between the Ricci flow and deep neural networks by dynamically stable Poincar\'e embeddings for neural manifolds. As a result, we prove that, if initial metrics have an $L^2$-norm perturbation which deviates from the Hyperbolic metric on the Poincar\'e ball, the scaled Ricci-DeTurck flow of such metrics smoothly and exponentially converges to the Hyperbolic metric. Specifically, the role of the Ricci flow is to serve as naturally evolving to the stable Poincar\'e ball that will then be mapped back to the Euclidean space. For such dynamically stable neural manifolds under the Ricci flow, the convergence of neural networks embedded with such manifolds is not susceptible to perturbations. And we show that such Ricci flow assisted neural networks outperform with their all Euclidean versions on image classification tasks (CIFAR datasets).