Dual Quaternion Rotational and Translational Equivariance in 3D Rigid Motion Modelling
Paper and Code
Oct 11, 2023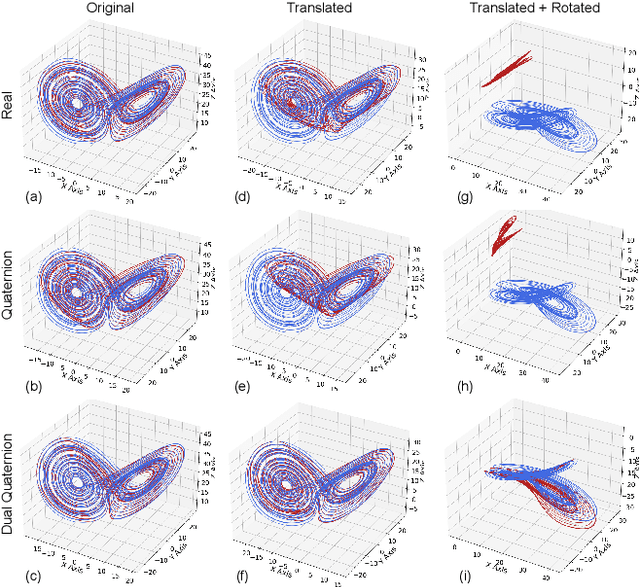

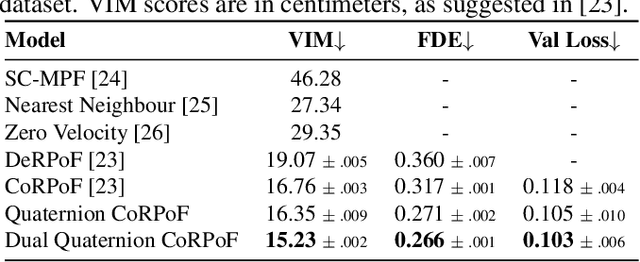
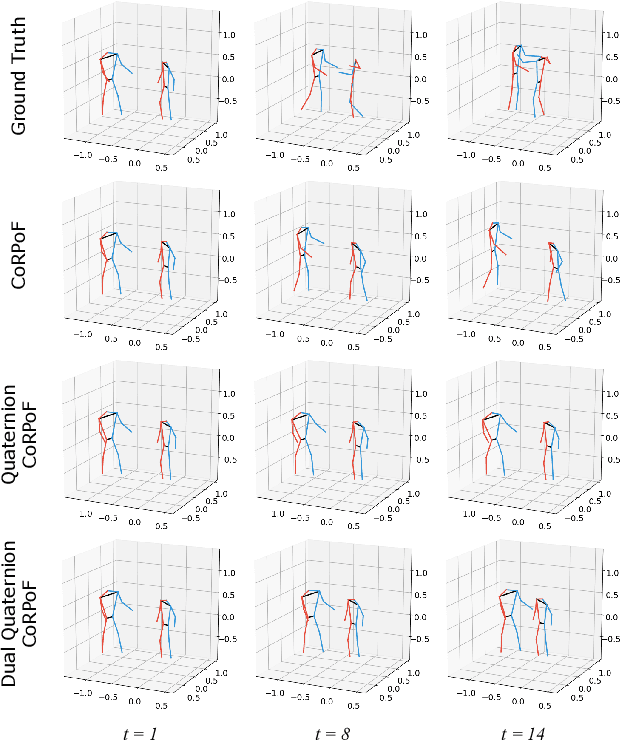
Objects' rigid motions in 3D space are described by rotations and translations of a highly-correlated set of points, each with associated $x,y,z$ coordinates that real-valued networks consider as separate entities, losing information. Previous works exploit quaternion algebra and their ability to model rotations in 3D space. However, these algebras do not properly encode translations, leading to sub-optimal performance in 3D learning tasks. To overcome these limitations, we employ a dual quaternion representation of rigid motions in the 3D space that jointly describes rotations and translations of point sets, processing each of the points as a single entity. Our approach is translation and rotation equivariant, so it does not suffer from shifts in the data and better learns object trajectories, as we validate in the experimental evaluations. Models endowed with this formulation outperform previous approaches in a human pose forecasting application, attesting to the effectiveness of the proposed dual quaternion formulation for rigid motions in 3D space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge