Domain Generalization Needs Stochastic Weight Averaging for Robustness on Domain Shifts

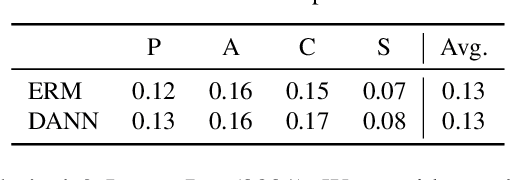
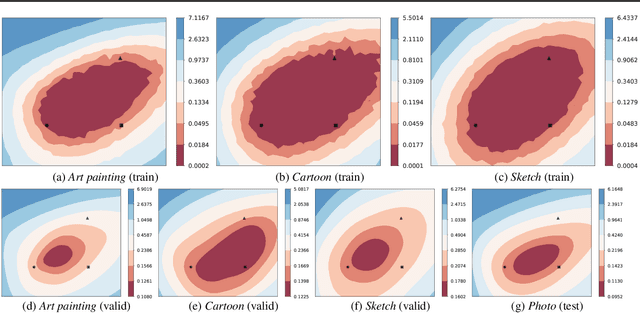
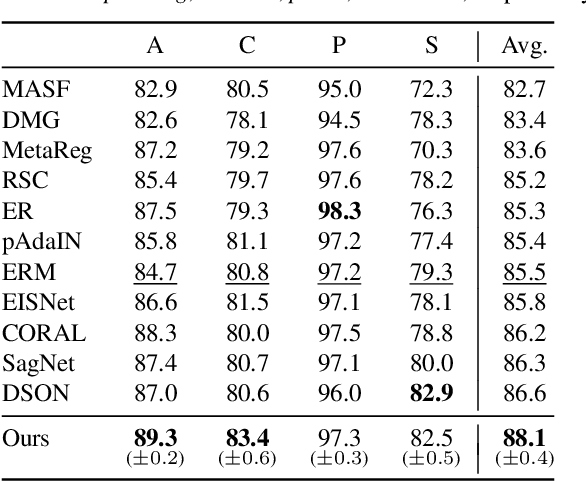
Domain generalization aims to learn a generalizable model to unseen target domains from multiple source domains. Various approaches have been proposed to address this problem. However, recent benchmarks show that most of them do not provide significant improvements compared to the simple empirical risk minimization (ERM) in practical cases. In this paper, we analyze how ERM works in views of domain-invariant feature learning and domain-specific gradient normalization. In addition, we observe that ERM converges to a loss valley shared over multiple training domains and obtain an insight that a center of the valley generalizes better. To estimate the center, we employ stochastic weight averaging (SWA) and provide theoretical analysis describing how SWA supports the generalization bound for an unseen domain. As a result, we achieve state-of-the-art performances over all of widely used domain generalization benchmarks, namely PACS, VLCS, OfficeHome, TerraIncognita, and DomainNet with large margins. Further analysis reveals how SWA operates on domain generalization tasks.