Distributionally Robust Neural Networks for Group Shifts: On the Importance of Regularization for Worst-Case Generalization
Paper and Code
Nov 20, 2019
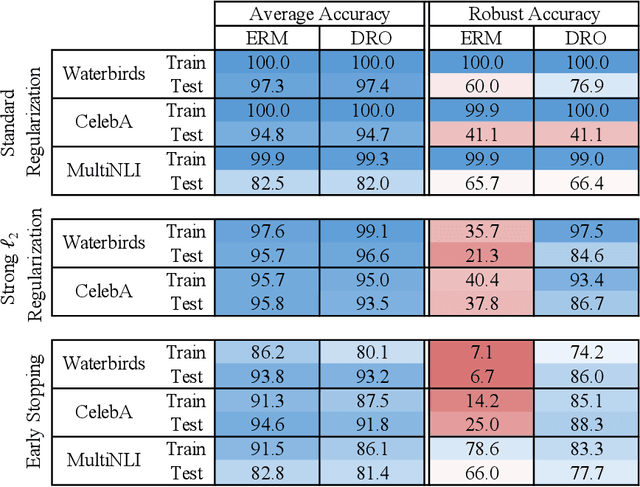

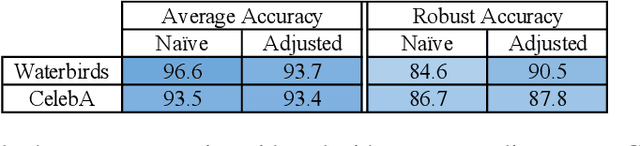
Overparameterized neural networks can be highly accurate on average on an i.i.d. test set yet consistently fail on atypical groups of the data (e.g., by learning spurious correlations that hold on average but not in such groups). Distributionally robust optimization (DRO) allows us to learn models that instead minimize the worst-case training loss over a set of pre-defined groups. However, we find that naively applying group DRO to overparameterized neural networks fails: these models can perfectly fit the training data, and any model with vanishing average training loss also already has vanishing worst-case training loss. Instead, their poor worst-case performance arises from poor generalization on some groups. By coupling group DRO models with increased regularization---stronger-than-typical $\ell_2$ regularization or early stopping---we achieve substantially higher worst-group accuracies, with 10-40 percentage point improvements on a natural language inference task and two image tasks, while maintaining high average accuracies. Our results suggest that regularization is critical for worst-group generalization in the overparameterized regime, even if it is not needed for average generalization. Finally, we introduce and give convergence guarantees for a stochastic optimizer for the group DRO setting, underpinning the empirical study above.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge