Distributionally Adaptive Meta Reinforcement Learning
Paper and Code
Oct 06, 2022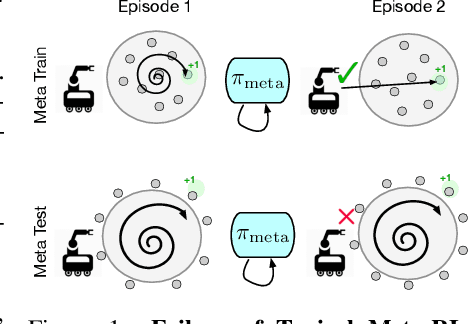

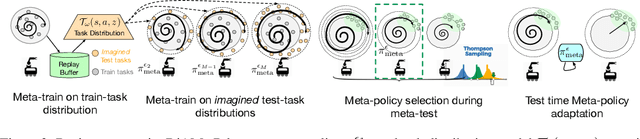
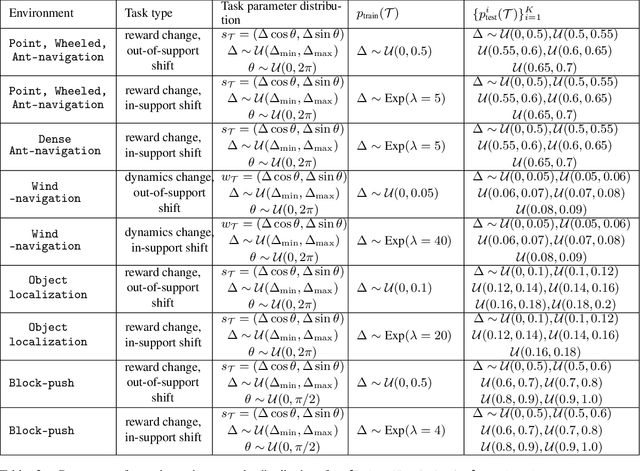
Meta-reinforcement learning algorithms provide a data-driven way to acquire policies that quickly adapt to many tasks with varying rewards or dynamics functions. However, learned meta-policies are often effective only on the exact task distribution on which they were trained and struggle in the presence of distribution shift of test-time rewards or transition dynamics. In this work, we develop a framework for meta-RL algorithms that are able to behave appropriately under test-time distribution shifts in the space of tasks. Our framework centers on an adaptive approach to distributional robustness that trains a population of meta-policies to be robust to varying levels of distribution shift. When evaluated on a potentially shifted test-time distribution of tasks, this allows us to choose the meta-policy with the most appropriate level of robustness, and use it to perform fast adaptation. We formally show how our framework allows for improved regret under distribution shift, and empirically show its efficacy on simulated robotics problems under a wide range of distribution shifts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge