Distributed Semi-supervised Fuzzy Regression with Interpolation Consistency Regularization
Paper and Code
Sep 18, 2022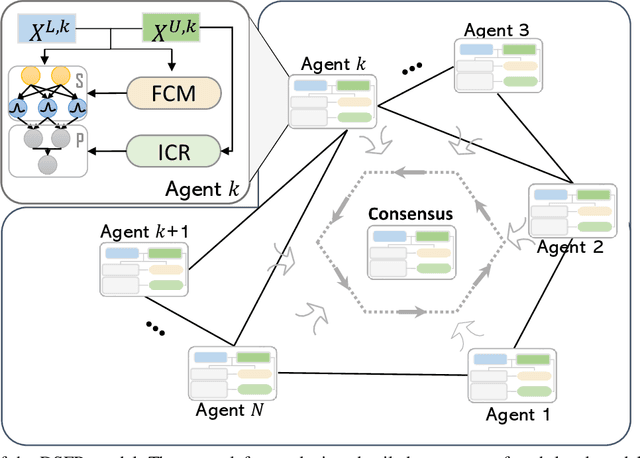
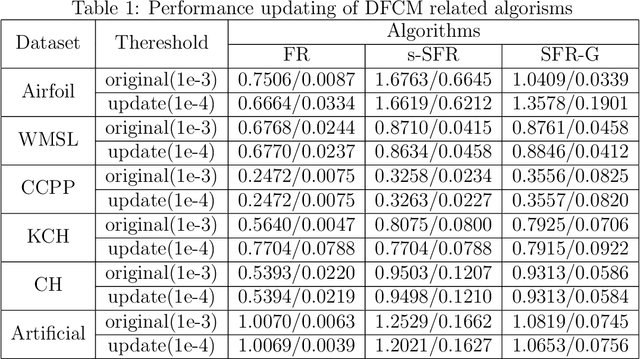
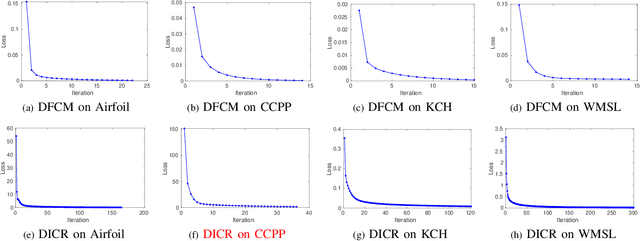
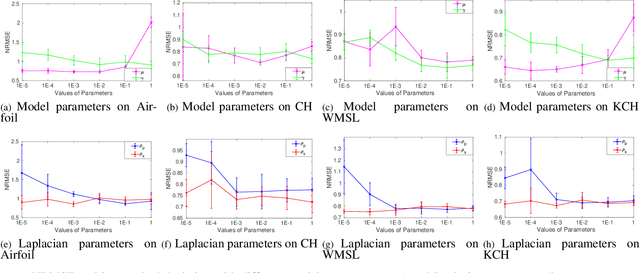
Recently, distributed semi-supervised learning (DSSL) algorithms have shown their effectiveness in leveraging unlabeled samples over interconnected networks, where agents cannot share their original data with each other and can only communicate non-sensitive information with their neighbors. However, existing DSSL algorithms cannot cope with data uncertainties and may suffer from high computation and communication overhead problems. To handle these issues, we propose a distributed semi-supervised fuzzy regression (DSFR) model with fuzzy if-then rules and interpolation consistency regularization (ICR). The ICR, which was proposed recently for semi-supervised problem, can force decision boundaries to pass through sparse data areas, thus increasing model robustness. However, its application in distributed scenarios has not been considered yet. In this work, we proposed a distributed Fuzzy C-means (DFCM) method and a distributed interpolation consistency regularization (DICR) built on the well-known alternating direction method of multipliers to respectively locate parameters in antecedent and consequent components of DSFR. Notably, the DSFR model converges very fast since it does not involve back-propagation procedure and is scalable to large-scale datasets benefiting from the utilization of DFCM and DICR. Experiments results on both artificial and real-world datasets show that the proposed DSFR model can achieve much better performance than the state-of-the-art DSSL algorithm in terms of both loss value and computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge