Distributed Exploration in Multi-Armed Bandits
Paper and Code
Nov 04, 2013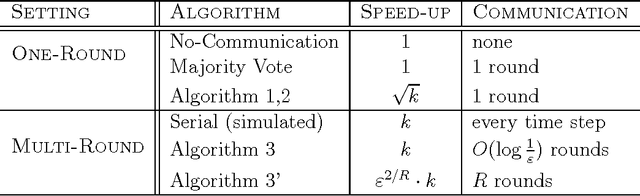
We study exploration in Multi-Armed Bandits in a setting where $k$ players collaborate in order to identify an $\epsilon$-optimal arm. Our motivation comes from recent employment of bandit algorithms in computationally intensive, large-scale applications. Our results demonstrate a non-trivial tradeoff between the number of arm pulls required by each of the players, and the amount of communication between them. In particular, our main result shows that by allowing the $k$ players to communicate only once, they are able to learn $\sqrt{k}$ times faster than a single player. That is, distributing learning to $k$ players gives rise to a factor $\sqrt{k}$ parallel speed-up. We complement this result with a lower bound showing this is in general the best possible. On the other extreme, we present an algorithm that achieves the ideal factor $k$ speed-up in learning performance, with communication only logarithmic in $1/\epsilon$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge