Distilling Double Descent
Paper and Code
Feb 13, 2021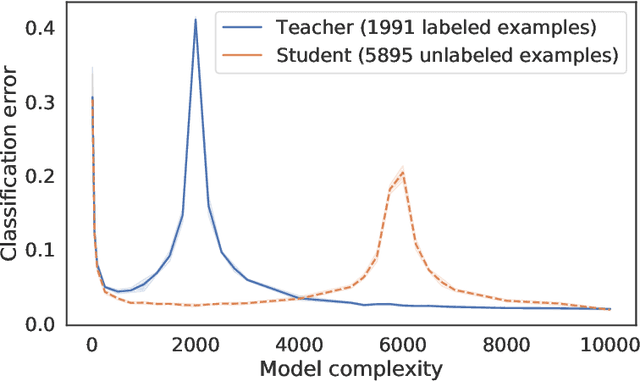
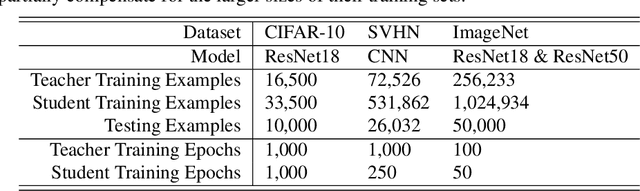
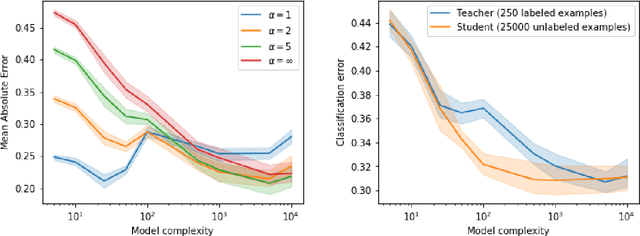
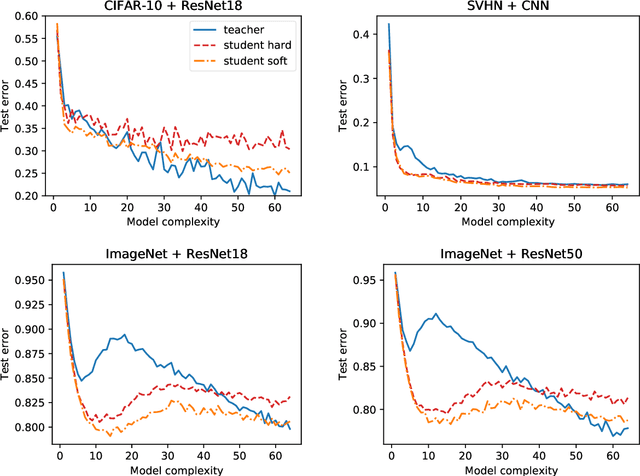
Distillation is the technique of training a "student" model based on examples that are labeled by a separate "teacher" model, which itself is trained on a labeled dataset. The most common explanations for why distillation "works" are predicated on the assumption that student is provided with \emph{soft} labels, \eg probabilities or confidences, from the teacher model. In this work, we show, that, even when the teacher model is highly overparameterized, and provides \emph{hard} labels, using a very large held-out unlabeled dataset to train the student model can result in a model that outperforms more "traditional" approaches. Our explanation for this phenomenon is based on recent work on "double descent". It has been observed that, once a model's complexity roughly exceeds the amount required to memorize the training data, increasing the complexity \emph{further} can, counterintuitively, result in \emph{better} generalization. Researchers have identified several settings in which it takes place, while others have made various attempts to explain it (thus far, with only partial success). In contrast, we avoid these questions, and instead seek to \emph{exploit} this phenomenon by demonstrating that a highly-overparameterized teacher can avoid overfitting via double descent, while a student trained on a larger independent dataset labeled by this teacher will avoid overfitting due to the size of its training set.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge