Differentiable Proximal Graph Matching
Paper and Code
May 26, 2024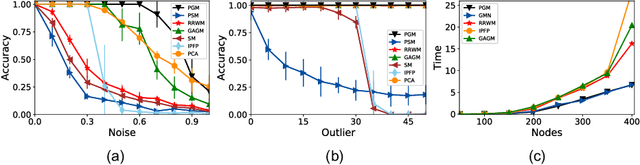

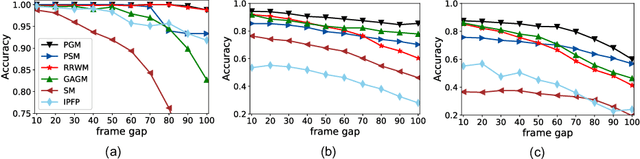
Graph matching is a fundamental tool in computer vision and pattern recognition. In this paper, we introduce an algorithm for graph matching based on the proximal operator, referred to as differentiable proximal graph matching (DPGM). Specifically, we relax and decompose the quadratic assignment problem for the graph matching into a sequence of convex optimization problems. The whole algorithm can be considered as a differentiable map from the graph affinity matrix to the prediction of node correspondence. Therefore, the proposed method can be organically integrated into an end-to-end deep learning framework to jointly learn both the deep feature representation and the graph affinity matrix. In addition, we provide a theoretical guarantee to ensure the proposed method converges to a stable point with a reasonable number of iterations. Numerical experiments show that PGM outperforms existing graph matching algorithms on diverse datasets such as synthetic data, and CMU House. Meanwhile, PGM can fully harness the capability of deep feature extractors and achieve state-of-art performance on PASCAL VOC keypoints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge