Differentiable Meta-Learning in Contextual Bandits

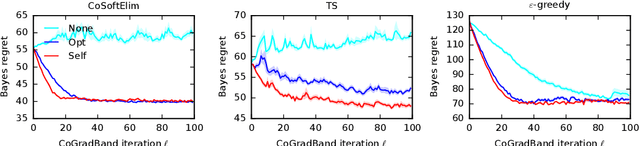
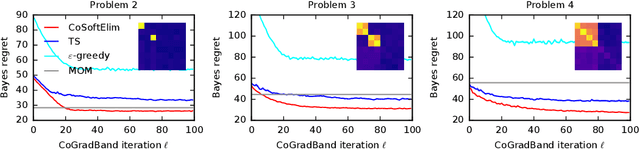
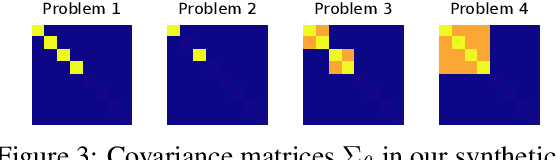
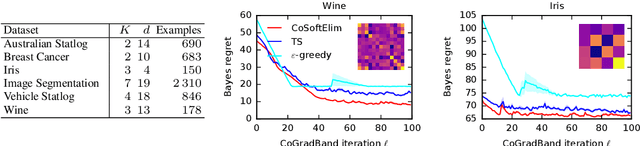
We study a contextual bandit setting where the learning agent has access to sampled bandit instances from an unknown prior distribution $\mathcal{P}$. The goal of the agent is to achieve high reward on average over the instances drawn from $\mathcal{P}$. This setting is of a particular importance because it formalizes the offline optimization of bandit policies, to perform well on average over anticipated bandit instances. The main idea in our work is to optimize differentiable bandit policies by policy gradients. We derive reward gradients that reflect the structure of our problem, and propose contextual policies that are parameterized in a differentiable way and have low regret. Our algorithmic and theoretical contributions are supported by extensive experiments that show the importance of baseline subtraction, learned biases, and the practicality of our approach on a range of classification tasks.