Differentiable Bandit Exploration
Paper and Code
Feb 17, 2020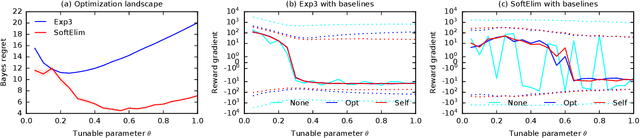
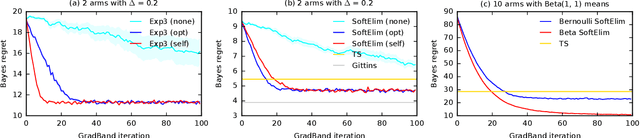
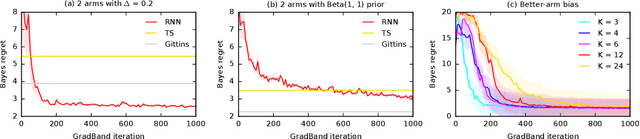
We learn bandit policies that maximize the average reward over bandit instances drawn from an unknown distribution $\mathcal{P}$, from a sample from $\mathcal{P}$. Our approach is an instance of meta-learning and its appeal is that the properties of $\mathcal{P}$ can be exploited without restricting it. We parameterize our policies in a differentiable way and optimize them by policy gradients - an approach that is easy to implement and pleasantly general. Then the challenge is to design effective gradient estimators and good policy classes. To make policy gradients practical, we introduce novel variance reduction techniques. We experiment with various bandit policy classes, including neural networks and a novel soft-elimination policy. The latter has regret guarantees and is a natural starting point for our optimization. Our experiments highlight the versatility of our approach. We also observe that neural network policies can learn implicit biases, which are only expressed through sampled bandit instances during training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge