DEMI: Discriminative Estimator of Mutual Information

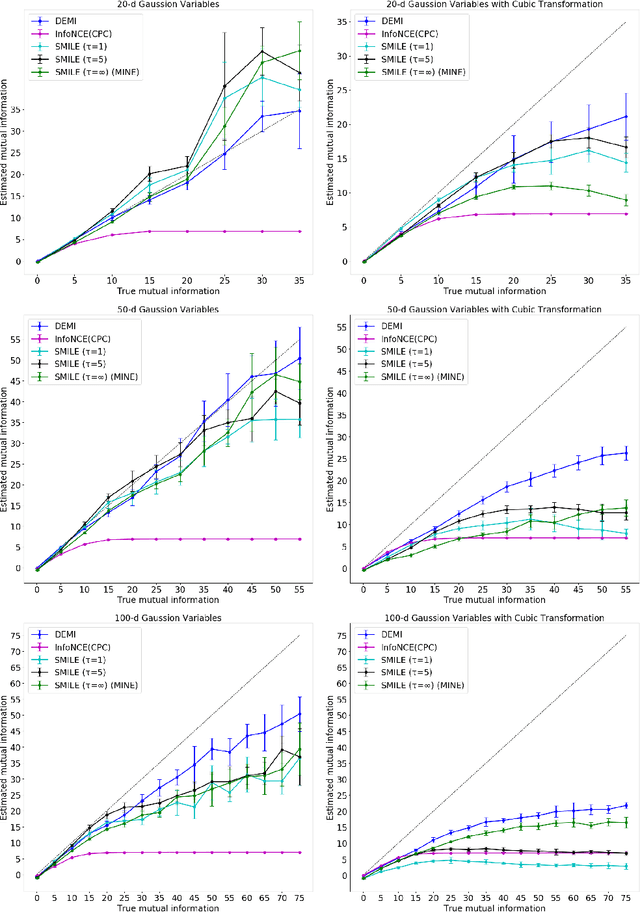
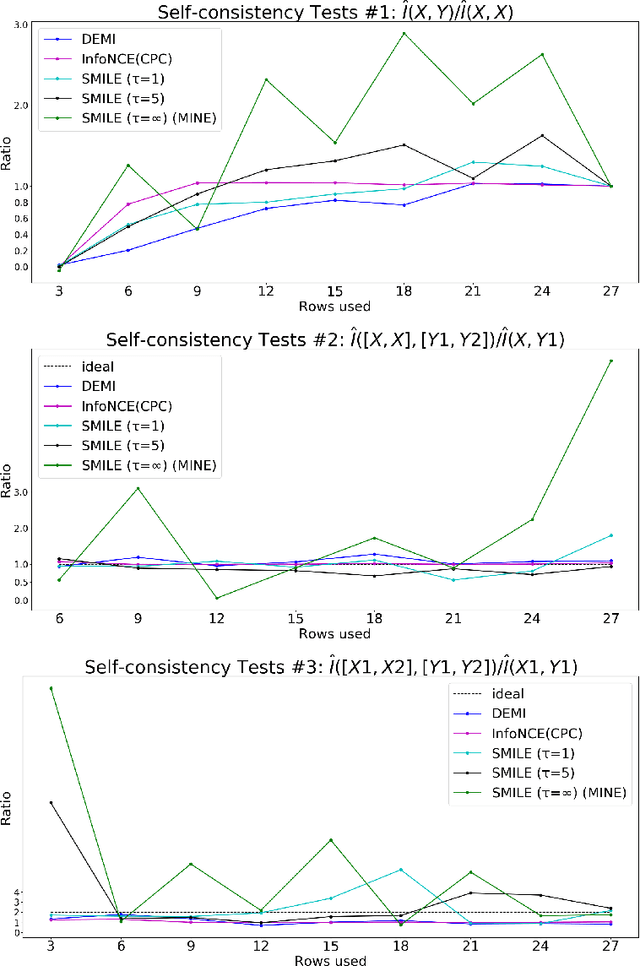
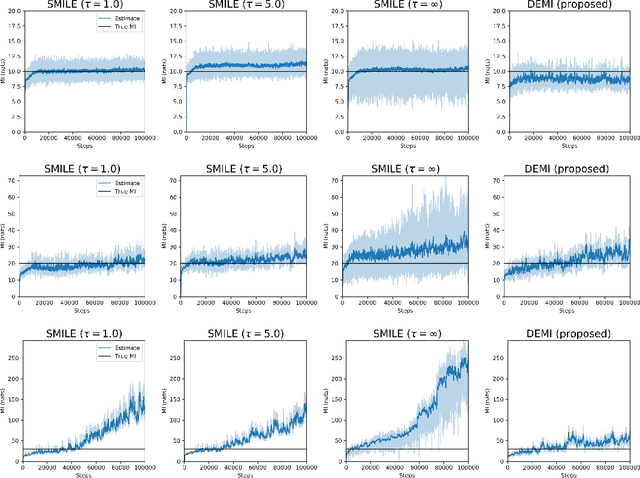
Estimating mutual information between continuous random variables is often intractable and extremely challenging for high-dimensional data. Recent progress has leveraged neural networks to optimize variational lower bounds on mutual information. Although showing promise for this difficult problem, the variational methods have been theoretically and empirically proven to have serious statistical limitations: 1) most of the approaches cannot make accurate estimates when the underlying mutual information is either low or high; 2) the resulting estimators may suffer from high variance. Our approach is based on training a classifier that provides the probability whether a data sample pair is drawn from the joint distribution or from the product of its marginal distributions. We use this probabilistic prediction to estimate mutual information. We show theoretically that our method and other variational approaches are equivalent when they achieve their optimum, while our approach does not optimize a variational bound. Empirical results demonstrate high accuracy and a good bias/variance tradeoff using our approach.